题目内容
 如图,在△ABC中,AB=AC,EF为△ABC的中位线,点G为EF的中点,连接BG,CG.
如图,在△ABC中,AB=AC,EF为△ABC的中位线,点G为EF的中点,连接BG,CG.(1)求证:BG=CG;
(2)当∠BGC=90°时,过点B作BD⊥AC,交GC于H,连接HF,求证:BH=FH+CF.
考点:全等三角形的判定与性质,三角形中位线定理
专题:证明题
分析:(1)根据等腰三角形的性质,可得∠ABC=∠ACB,有中位线定理和点G为EF的中点可证明△BEG≌△CFG,从而得出结论;
(2)延长BG交AC于M,根据题意可证明△BGH≌CGM,得出BH=CM,GH=GM,还可证明△GMF≌△GHF,则MF=HF,即可证明BH=FH+CF.
(2)延长BG交AC于M,根据题意可证明△BGH≌CGM,得出BH=CM,GH=GM,还可证明△GMF≌△GHF,则MF=HF,即可证明BH=FH+CF.
解答: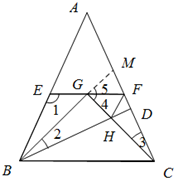 证明:(1)∵AB=AC,
证明:(1)∵AB=AC,
∴∠ABC=∠ACB,
又∵EF为中位线,
∴BE=
AB=CF,EF∥BC,
∴∠1+∠ABC=∠EFC+∠ACB=180°,
∴∠1=∠EFC,
又∵G为EF的中点,
∴EG=GF,
∴在△BEG和△CFG中,
∴△BEG≌△CFG,
∴BG=CG;
(2)延长BG交AC于M,
∵∠BGC=90°,BD⊥AC,
∴∠2=90°-∠GHB=90°-∠DHC=∠3,
在△BGH和CGM中,
∴△BGH≌CGM,
∴BH=CM,GH=GM
又∵EF∥BC,
∴∠4=∠GCB=45°,
∴∠5=90°-∠4=45°=∠4
在△GMF和△GHF中
,
∴△GMF≌△GHF,
∴MF=HF,
∴BH=CM=MF+FC=FH+FC.
 证明:(1)∵AB=AC,
证明:(1)∵AB=AC,∴∠ABC=∠ACB,
又∵EF为中位线,
∴BE=
| 1 |
| 2 |
∴∠1+∠ABC=∠EFC+∠ACB=180°,
∴∠1=∠EFC,
又∵G为EF的中点,
∴EG=GF,
∴在△BEG和△CFG中,
|
∴△BEG≌△CFG,
∴BG=CG;
(2)延长BG交AC于M,
∵∠BGC=90°,BD⊥AC,
∴∠2=90°-∠GHB=90°-∠DHC=∠3,
在△BGH和CGM中,
|
∴△BGH≌CGM,
∴BH=CM,GH=GM
又∵EF∥BC,
∴∠4=∠GCB=45°,
∴∠5=90°-∠4=45°=∠4
在△GMF和△GHF中
|
∴△GMF≌△GHF,
∴MF=HF,
∴BH=CM=MF+FC=FH+FC.
点评:本题考查了全等三角形的判定和性质以及三角形的中位线定理,是中考常见题型,熟练掌握全等三角形的判定方法是解题的关键.

练习册系列答案
相关题目
①若|-a|=a,则a>0;②整数和分数统称有理数;③过一点,有且只有一条直线与已知直线平行;④2x2-xy+y2是二次三项式;⑤几个有理数相乘,当负因数的个数是奇数时,积一定为负数;⑥AB=BC,则B是AC中点.其中判断正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
| A、1cm,2cm,3cm |
| B、4cm,2cm,3cm |
| C、5cm,5cm,11cm |
| D、4cm,8cm,3cm |
 在一次数学课上,王老师在黑板上画出如图,并写下了四个等式:①AB=DC;②BE=CE;③∠B=∠C;④∠BAE=∠CDE.
在一次数学课上,王老师在黑板上画出如图,并写下了四个等式:①AB=DC;②BE=CE;③∠B=∠C;④∠BAE=∠CDE.