题目内容
9.函数y=2|x-3|与y=x-a的图象围成一个平面区域,求实数a的取值范围及这个区域的面积.分析 分类讨论:x≥3,x<3,根据函数图象有交点,可得不等式,根据解不等式,可得答案;
根据三角形面积的和差,可得答案.
解答 解:如图: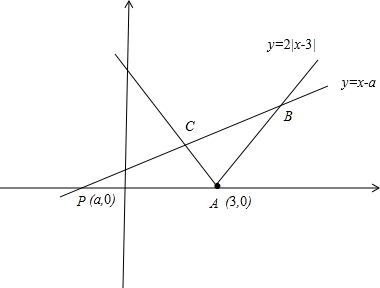 ,
,
y=2|x-3|的图象是端点为A(3,0)的两条向上的射线,
y=x-a的图象是过P(a,0)倾斜角为45°的直线.
先求两个图象交点的横坐标:
①当x≥3时,2(x-3)=x-a,x=6-a;6-a≥3,解得a≤3;
②当x<3时,2(3-x)=x-a,x=$\frac{6+a}{3}$,$\frac{6+a}{3}$<3,解得a<3,
∴y=2|x-3|与y=x-a的图象围成一个平面区域,
a<3;
这时,交点B(6-a,6-2a),C($\frac{6+a}{3}$,$\frac{6-2a}{3}$),
S△ABC=S△ABP-S△ACP
=$\frac{1}{2}$(3-a)[(6-2a)-$\frac{6-2a}{3}$]
=$\frac{2}{3}$(3-a)2.
点评 本题考查了一次函数图象,根据题意画出函数图象是解题关键,利用函数解析式得出交点的坐标,再解不等式得出a的取值范围.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
19.化简$\frac{1+\sqrt{2-\sqrt{2}}+\sqrt{2-\sqrt{3}}}{\sqrt{3}+\sqrt{2+\sqrt{2}}+\sqrt{2+\sqrt{3}}}$,可得( )
| A. | $\sqrt{3}$-$\sqrt{2}$ | B. | $\frac{\sqrt{2}+1}{2}$ | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-1 |
 △ABC中,∠BAC=70°,BC=12,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,求:∠EAN的度数.
△ABC中,∠BAC=70°,BC=12,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点N,求:∠EAN的度数.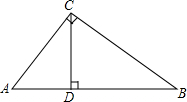 如图所示,AC⊥BC,CD⊥AB,AC=5cm,BC=12cm,AB=13cm,则点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.
如图所示,AC⊥BC,CD⊥AB,AC=5cm,BC=12cm,AB=13cm,则点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.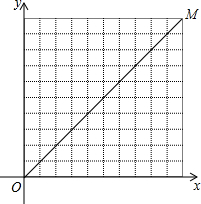 如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于y轴的抛物线与网格对角线OM的两个交点为A,B,其顶点为C,如果△ABC是该抛物线的内接格点三角形,AB=3$\sqrt{2}$,且点A,B,C的横坐标xA,xB,xC满足xA<xC<xB,那么符合上述条件的抛物线条数是( )
如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于y轴的抛物线与网格对角线OM的两个交点为A,B,其顶点为C,如果△ABC是该抛物线的内接格点三角形,AB=3$\sqrt{2}$,且点A,B,C的横坐标xA,xB,xC满足xA<xC<xB,那么符合上述条件的抛物线条数是( )