题目内容
 如图,某天晚上8点时,一台风中心位于点O正北方向160km点A处,台风中心以每小时20
如图,某天晚上8点时,一台风中心位于点O正北方向160km点A处,台风中心以每小时20| 2 |
(1)汽车行驶了多少小时后受到台风影响?
(2)汽车受到台风影响的时间有多长?
考点:勾股定理的应用
专题:
分析:(1)以O为原点,OA所在直线为y轴,汽车行驶的路线为x轴,作出坐标系,设当台风中心在M点,汽车在N点开始,汽车受到影响,设运动时间是t小时,即可利用t表示出M、N的坐标,根据MN=120,即可得到一个关于t的方程,解方程即可求得t的值;
(2)将两个t的值相减即可求解.
(2)将两个t的值相减即可求解.
解答: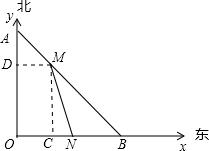 解:(1)以O为原点,OA所在直线为y轴,汽车行驶的路线为x轴,作出坐标系.
解:(1)以O为原点,OA所在直线为y轴,汽车行驶的路线为x轴,作出坐标系.
设当台风中心在M点,汽车在N点开始,汽车受到影响,设运动时间是t小时,过M作MC⊥x轴与C,作MD⊥y轴.
则△ADM是等腰直角三角形,AM=20
t,则AD=DM=
AM=20t,
因而M的坐标是:(20t,160-20t),
N的坐标是:(40t,0).
汽车受到影响,则MN=120千米,
即(40t-20t)2+(160-20t)2=1202,
即t2-8t+14=0,
解得x1=4-
,x2=4+
.
答:汽车行驶了(4-
)小时后受到台风影响
(2)(4+
)-(4-
)=2
(小时)
答:汽车受到台风影响的时间有2
小时.
 解:(1)以O为原点,OA所在直线为y轴,汽车行驶的路线为x轴,作出坐标系.
解:(1)以O为原点,OA所在直线为y轴,汽车行驶的路线为x轴,作出坐标系.设当台风中心在M点,汽车在N点开始,汽车受到影响,设运动时间是t小时,过M作MC⊥x轴与C,作MD⊥y轴.
则△ADM是等腰直角三角形,AM=20
| 2 |
| ||
| 2 |
因而M的坐标是:(20t,160-20t),
N的坐标是:(40t,0).
汽车受到影响,则MN=120千米,
即(40t-20t)2+(160-20t)2=1202,
即t2-8t+14=0,
解得x1=4-
| 2 |
| 2 |
答:汽车行驶了(4-
| 2 |
(2)(4+
| 2 |
| 2 |
| 2 |
答:汽车受到台风影响的时间有2
| 2 |
点评:本题考查了勾股定理,把判断是否受影响的问题转化成一元二次方程的解得问题是关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 如图,已知AB∥CD,E是AB上一点,DE平分∠BEC交CD于D,∠C=80°,则∠D的度数是( )
如图,已知AB∥CD,E是AB上一点,DE平分∠BEC交CD于D,∠C=80°,则∠D的度数是( )| A、40° | B、45° |
| C、50° | D、55° |
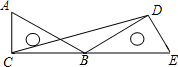 把两块含30°角的相同的直角三角板按如图所示摆放,使点C、B、E在同一直线上,连接CD,则∠CDB的度数为( )
把两块含30°角的相同的直角三角板按如图所示摆放,使点C、B、E在同一直线上,连接CD,则∠CDB的度数为( )| A、15° | B、18° |
| C、25° | D、30° |
 如图,点A、B、C在同一条直线上,分别以AB、BC为边在直线AC的同侧作等边三角形△ABD、△BCE.连接AE、DC,AE与DC所在直线相交于F,连接FB.判断线段FB、FE与FC之间的数量关系,并证明你的结论.
如图,点A、B、C在同一条直线上,分别以AB、BC为边在直线AC的同侧作等边三角形△ABD、△BCE.连接AE、DC,AE与DC所在直线相交于F,连接FB.判断线段FB、FE与FC之间的数量关系,并证明你的结论.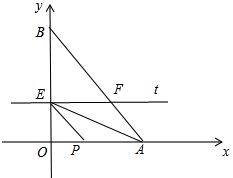 如图,在平面直角坐标系中,以点A坐标为(6,0),点B坐标为(0,8),动点P从点A开始沿折线AO-OB-BA运动,点P在AO,OB,BA边上运动的速度分别为每秒3,4,5个单位,直线l从与OA重合的位置开始,以每秒
如图,在平面直角坐标系中,以点A坐标为(6,0),点B坐标为(0,8),动点P从点A开始沿折线AO-OB-BA运动,点P在AO,OB,BA边上运动的速度分别为每秒3,4,5个单位,直线l从与OA重合的位置开始,以每秒 已知在纸面上有一数轴(如图),折叠纸面.
已知在纸面上有一数轴(如图),折叠纸面.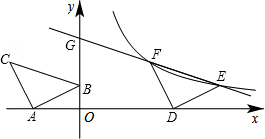 如图,把一块等腰直角三角板ABC放在平面直角坐标系的第二象限内,若∠A=90°,AB=AC,且A、B两点的坐标分别为(-4,0)、(0,2).
如图,把一块等腰直角三角板ABC放在平面直角坐标系的第二象限内,若∠A=90°,AB=AC,且A、B两点的坐标分别为(-4,0)、(0,2).