题目内容
19.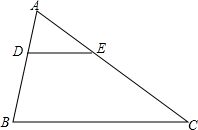 在△ABC中,DE∥BC,EC=4AD,DB=AE=4cm,BC=10cm,则DE的长$\frac{10}{3}$cm.
在△ABC中,DE∥BC,EC=4AD,DB=AE=4cm,BC=10cm,则DE的长$\frac{10}{3}$cm.
分析 由DE∥BC,根据平行线分线段成比例定理,可求出AD的长,再求出AD:AB,由△ADE∽△ABC,可知$\frac{AD}{AB}=\frac{DE}{BC}$,即可求出DE的长.
解答 解:∵DE∥BC,
∴$\frac{AD}{DB}=\frac{AE}{EC}$,
又∵EC=4AD,DB=AE=4cm,
∴$\frac{AD}{4}=\frac{4}{4AD}$,
解得:AD=2,
∴AD:AB=2:6=1:3,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}=\frac{DE}{BC}$,
∵BC=10cm,
∴$\frac{1}{3}=\frac{DE}{10}$,
解得:DE=$\frac{10}{3}$cm.
故答案为:$\frac{10}{3}$.
点评 本题主要考查平行线分线段成比例定理以及相似三角形的判定与性质的理解及运用,正确理解定理是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.某市2010年平均房价为每平方米4000元.连续两年增长后,2012年平均房价达到每平方米5500元.设这两年平均房价年平均增长率为x,根据题意,下面所列方程正确的是( )
| A. | 5500(1+x)2=4000 | B. | 5500(1-x)2=4000 | C. | 4000(1-x)2=5500 | D. | 4000(1+x)2=5500 |
8.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{12}$ | B. | $\sqrt{{x}^{2}+2xy-{y}^{2}}$ | C. | $\sqrt{2{x}^{3}}$ | D. | $\sqrt{\frac{x}{2}}$ |
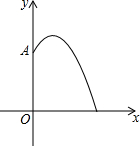 某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=-x2+2x+$\frac{5}{4}$,则下列结论:
某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=-x2+2x+$\frac{5}{4}$,则下列结论: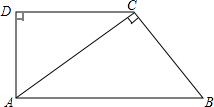 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm, 如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第二限的图象经过点B,若OA2-AB2=10,则k的值为-5.
如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第二限的图象经过点B,若OA2-AB2=10,则k的值为-5.