题目内容
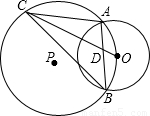
已知:如图,⊙P与⊙O相交于点A、B,且⊙P经过点O,点C是⊙P的优弧AB上任意一点(不与点A、B重合),弦OC交公共弦AB于点D,连接CA、CB.(1)求证:CD•CO=CA•CB;
(2)当点C在⊙P上何位置时,直线CA与⊙O相切?并说明理由;
(3)当∠ACB等于60°时,两圆半径有什么关系?并说明理由.
【答案】分析:(1)首先证明△ACO∽△DCB,根据相似三角形的性质可得 =
= ,进而得到CD•CO=CA•CB;
,进而得到CD•CO=CA•CB;
(2)连接OP,并延长与⊙P交于点E.若点C在点E位置时,直线CA与⊙O相切,然后根据直径所对的圆周角是直角可得∠OAE=90°,进而得到OA⊥EA,即EA与⊙O相切;
(3)当∠ACB=60°时,两圆半径相等,作直径OE,连接BE,AE,OA,然后证明∠AEO=30°,再根据直角三角形中,30°角所对的直角边等于斜边的一半可得OA= OE,进而得到OP=OA.
OE,进而得到OP=OA.
解答:(1)证明:在⊙O中,∵AO=BO,
∴ =
= ,
,
∴∠ACO=∠DCB,
又∵∠1=∠2,
∴△ACO∽△DCB,
∴ =
= ,
,
∴CD•CO=CA•CB;
(2)解:连接OP,并延长与⊙P交于点E.
若点C在点E位置时,直线CA与⊙O相切,
理由:连接AE,
∵EO是⊙P的直径,
∴∠EAO=90°,
∴OA⊥EA,
∴EA与⊙O相切,
即点C在点E位置时,直线CA与⊙O相切.
(3)当∠ACB=60°时,两圆半径相等.理由:
解:作直径OE,连接BE,AE,OA,
∵∠AEB=∠ACB=60°,PO垂直平分AB,
∴ =
= ,
,
∴∠AEO=∠BEO,
∴∠AEO=30°,
∵OE是直径,
∴∠EAO=90°,
∴OA= OE,
OE,
∴OA=PO,
∴当∠ACB=60°时,两圆半径相等.
点评:本题主要考查了圆的综合,关键是掌握等弧所对的圆周角相等;直径所对的圆周角等于90°;直角三角形中,30°角所对的直角边等于斜边的一半,切线的判定、相似三角形的判定与性质等知识.具有一定的综合性.
 =
= ,进而得到CD•CO=CA•CB;
,进而得到CD•CO=CA•CB;(2)连接OP,并延长与⊙P交于点E.若点C在点E位置时,直线CA与⊙O相切,然后根据直径所对的圆周角是直角可得∠OAE=90°,进而得到OA⊥EA,即EA与⊙O相切;
(3)当∠ACB=60°时,两圆半径相等,作直径OE,连接BE,AE,OA,然后证明∠AEO=30°,再根据直角三角形中,30°角所对的直角边等于斜边的一半可得OA=
 OE,进而得到OP=OA.
OE,进而得到OP=OA.解答:(1)证明:在⊙O中,∵AO=BO,
∴
 =
= ,
,∴∠ACO=∠DCB,
又∵∠1=∠2,
∴△ACO∽△DCB,
∴
 =
= ,
,∴CD•CO=CA•CB;
(2)解:连接OP,并延长与⊙P交于点E.
若点C在点E位置时,直线CA与⊙O相切,
理由:连接AE,
∵EO是⊙P的直径,
∴∠EAO=90°,

∴OA⊥EA,
∴EA与⊙O相切,
即点C在点E位置时,直线CA与⊙O相切.
(3)当∠ACB=60°时,两圆半径相等.理由:
解:作直径OE,连接BE,AE,OA,
∵∠AEB=∠ACB=60°,PO垂直平分AB,
∴
 =
= ,
,∴∠AEO=∠BEO,
∴∠AEO=30°,
∵OE是直径,
∴∠EAO=90°,
∴OA=
 OE,
OE,∴OA=PO,
∴当∠ACB=60°时,两圆半径相等.
点评:本题主要考查了圆的综合,关键是掌握等弧所对的圆周角相等;直径所对的圆周角等于90°;直角三角形中,30°角所对的直角边等于斜边的一半,切线的判定、相似三角形的判定与性质等知识.具有一定的综合性.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
 21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.
21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.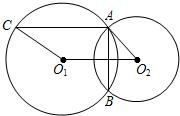 ,⊙O2的半径为
,⊙O2的半径为 14、已知:如图,⊙O1与⊙O2外切于点P,⊙O1的半径为3,且O1O2=8,则⊙O2的半径R=
14、已知:如图,⊙O1与⊙O2外切于点P,⊙O1的半径为3,且O1O2=8,则⊙O2的半径R= (1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D.
(1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D. 已知:如图,⊙O1与⊙O2相交于A,B两点.求证:直线O1O2垂直平分AB.
已知:如图,⊙O1与⊙O2相交于A,B两点.求证:直线O1O2垂直平分AB.