题目内容
4．
如图，AD是△ABC的中线，E、G分别是AB，AC中点，GF∥AD交ED的延长线于点F．（1）猜想：EF与AC有怎样的关系？
（2）试证明你的猜想．
分析 （1）根据题意进行猜测；
（2）根据三角形中位线定理、平行四边形的判定和性质定理进行证明．
解答 解：（1）EF=AC，EF∥AC，
（2）证明：∵AD是△ABC的中线，E是AB中点，
∴DE∥AC，DE=$\frac{1}{2}$AC，
∵GF∥AD，DE∥AC，
∴四边形AGFD是平行四边形，
∴AG=DF，
∴EF=AC，EF∥AC．
点评 本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．
练习册系列答案
科学实验活动册系列答案
相关题目
已知二次函数y=x2+（2m-2）x+m2-2m-3（m是常数）的图象与x轴交于A，B两点（点A在点B的左边）．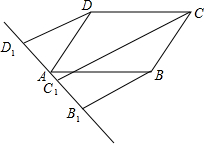
如图，直线l过?ABCD的顶点A，点D1、C1、B1都在直线l上，且DD1∥CC1∥BB1，求证：CC1=DD1+BB1．
如图，在△ABC中，D，E，F分别是AB，BC，CA的中点，AC=10，BC=14，求四边形DECF的周长．
如图，已知AB∥CD，∠1=140°，则∠2=40°．
如图，垂直于地面的灯柱AB被一钢缆CD固定，CD与地面成45°夹角（∠CDB=45°）；为了使灯柱更牢固，在C点上方2米处再新加固另一条钢线ED，ED与地面成53°夹角（∠EDB=53°），求线段ED的长．（结果精确到0.1米，参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）