题目内容
2.已知抛物线y=(x-1)2+2的图象上有A($\sqrt{3},{y}_{1}$),B(3,y2),C(-5,y3)三个点,则y1,y2,y3的大小关系是( )| A. | y3>y2>y1 | B. | y3>y1>y2 | C. | y2>y1>y3 | D. | y1>y2>y3 |
分析 先确定出抛物线的对称轴为x=1,再根据二次函数的增减性和对称性解答.
解答 解:∵抛物线y=(x-1)2+2的对称轴为x=1,a=1>0,
∴x<1时,y随x的增大而减小,x>1时,y随x的增大而增大,
∵C(-5,y3),
∴对称点的坐标为(7,y3),
∴y1<y2<y3.
故选A.
点评 本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的增减性和对称性,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.点P(1,-3)所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.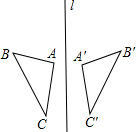 如图,△ABC与△A′B′C′关于直线l对称,∠A=98°,∠C′=28°,则∠B的度数为( )
如图,△ABC与△A′B′C′关于直线l对称,∠A=98°,∠C′=28°,则∠B的度数为( )
 如图,△ABC与△A′B′C′关于直线l对称,∠A=98°,∠C′=28°,则∠B的度数为( )
如图,△ABC与△A′B′C′关于直线l对称,∠A=98°,∠C′=28°,则∠B的度数为( )| A. | 28° | B. | 54° | C. | 74° | D. | 78° |
17. 如图,光源P在水平放置的横杆AB的正上方,AB在灯光下的影子CD也呈水平状态,AB=2m,CD=6m,点P到CD的距离是3.9m,则AB与CD之间的距离是( )
如图,光源P在水平放置的横杆AB的正上方,AB在灯光下的影子CD也呈水平状态,AB=2m,CD=6m,点P到CD的距离是3.9m,则AB与CD之间的距离是( )
 如图,光源P在水平放置的横杆AB的正上方,AB在灯光下的影子CD也呈水平状态,AB=2m,CD=6m,点P到CD的距离是3.9m,则AB与CD之间的距离是( )
如图,光源P在水平放置的横杆AB的正上方,AB在灯光下的影子CD也呈水平状态,AB=2m,CD=6m,点P到CD的距离是3.9m,则AB与CD之间的距离是( )| A. | 2.6m | B. | 2m | C. | 1.3m | D. | 1m |
7.某商人开始时,将进价为每件8元的某种商品按每件10元出售,每天可销出100件,他想采用提高售价的办法来增加利润,经试验,发现这种商品每件每提高1元,每天的销售量就会减少10件,为了能使一天所得的利润最大,他应将售价定为( )
| A. | 4元 | B. | 13元 | C. | 14元 | D. | 15元 |
11. 如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
 如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |