题目内容
5.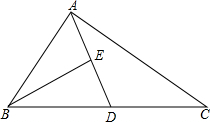 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)若△ABC的面积为40,BD=5,则E到BC边的距离为多少.
分析 (1)根据三角形内角与外角的性质解答即可;
(2)过E作BC边的垂线即可得:E到BC边的距离为EF的长,然后过A作BC边的垂线AG,再根据三角形中位线定理求解即可.
解答 解:(1)∵∠BED是△ABE的外角,
∴∠BED=∠ABE+∠BAD=15°+40°=55°;
(2)过E作BC边的垂线,F为垂足,则EF为所求的E到BC边的距离,
过A作BC边的垂线AG,
∴AD为△ABC的中线,BD=5,
∴BC=2BD=2×5=10,
∵△ABC的面积为40,
∴$\frac{1}{2}$BC•AG=40,即$\frac{1}{2}$×10•AG=40,解得AG=8,
∵EF⊥BC于F,
∴EF∥AG,
∵E为AD的中点,
∴EF是△AGD的中位线,
∴EF=$\frac{1}{2}$AG=$\frac{1}{2}$×8=4.
∴E到BC边的距离为4.
点评 本题考查了三角形外角的性质、三角形中位线定理及三角形的面积公式,涉及面较广,但难度适中.添加适当的辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.如果分式$\frac{3x+3y}{xy}$中的x,y都扩大到原来的3倍,那么分式的值( )
| A. | 不变 | B. | 扩大到原来的6倍 | ||
| C. | 扩大到原来的3倍 | D. | 缩小到原来的$\frac{1}{3}$倍 |
15.方程组$\left\{\begin{array}{l}{3x=2y}\\{x+y=50}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=10}\\{y=40}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=15}\\{y=35}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=20}\\{y=30}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=30}\\{y=20}\end{array}\right.$ |
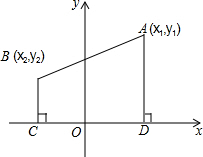 如图,A(x1,y1),B (x2,y2)是直角坐标系中的任意两点,AD,BC都垂直于x轴,点D,C分别为垂足
如图,A(x1,y1),B (x2,y2)是直角坐标系中的任意两点,AD,BC都垂直于x轴,点D,C分别为垂足
