题目内容
如图,已知△ABC内接于⊙O,AC是⊙O的直径,D是 的中点,过点D作直线BC的垂线,分别交CB、CA的延长线E、F
的中点,过点D作直线BC的垂线,分别交CB、CA的延长线E、F
(1)求证:EF是⊙O的切线;
(2)若EF=12,EC=9,求⊙O的半径.
(1)要证EF是⊙O的切线,只要连接OD,再证OD⊥EF即可;(2)
解析试题分析:(1)要证EF是⊙O的切线,只要连接OD,再证OD⊥EF即可;
(2)先根据勾股定理求出CF的长,再根据相似三角形的判定和性质求出⊙O的半径.
(1)连接OD交于AB于点G.
∵D是 的中点,OD为半径,
的中点,OD为半径,
∴AG=BG.
∵AO=OC,
∴OG是△ABC的中位线.
∴OG∥BC,
即OD∥CE.
又∵CE⊥EF,
∴OD⊥EF,
∴EF是⊙O的切线;
(2)在Rt△CEF中,EF=12,EC=9
∴CF=15
设半径OC=OD=r,则OF=15-r,
∵OD∥CE,
∴△FOD∽△FCE,
∴ ,解得
,解得
即⊙O的半径为 .
.
考点:切线的判定,相似三角形的判定和性质
点评:要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
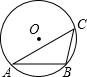 如图,已知△ABC内接于⊙O,∠C=45°,AB=4,则⊙O的半径为
如图,已知△ABC内接于⊙O,∠C=45°,AB=4,则⊙O的半径为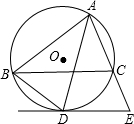 如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,过D作⊙O的切线与AC的延长线交于点E.
如图,已知△ABC内接于⊙O,AD平分∠BAC,交⊙O于点D,过D作⊙O的切线与AC的延长线交于点E. (2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N.
(2013•樊城区模拟)如图,已知△ABC内接于⊙O,弦AD交BC于E,过点D的切线MN交直线AB于M,交直线AC于N. 如图,已知△ABC内接于⊙O,AE平分∠BAC,且AD⊥BC于点D,连接OA.
如图,已知△ABC内接于⊙O,AE平分∠BAC,且AD⊥BC于点D,连接OA. 如图,已知△ABC内接于⊙O,AB=AC,∠A=36°,CD是⊙O的直径,求∠ACD的度数.
如图,已知△ABC内接于⊙O,AB=AC,∠A=36°,CD是⊙O的直径,求∠ACD的度数.