题目内容
14.若$\frac{a}{b}$=$\frac{3}{5}$,则$\frac{a+2b}{3a-b}$=$\frac{13}{4}$.分析 根据等式的性质,可用b表示a,根据分式的性质,可得答案.
解答 解:两边都乘以b,得
a=$\frac{3}{5}$b,
$\frac{a+2b}{3a-b}$=$\frac{\frac{3}{5}b+2b}{3×\frac{3}{5}b-b}$=$\frac{13}{4}$,
故答案为:$\frac{13}{4}$.
点评 本题考查了比例的性质,利用等式的性质得出a=$\frac{3}{5}$b是解题关键,又利用了分式的性质.

练习册系列答案
相关题目
4.若a2=(-3)2,那么a等于( )
| A. | -3 | B. | 3 | C. | 9 | D. | 3或-3 |
4.分式$\frac{1}{x-2}$无意义,则x的取值范围是( )
| A. | x>2 | B. | x=2 | C. | x≠2 | D. | x<2 |
 将如图所示的长方形绕图中的虚线旋转360°得到的几何体是( )
将如图所示的长方形绕图中的虚线旋转360°得到的几何体是( )



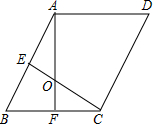 如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,AF、CE相交于点O,则∠AOC=120°.
如图,在菱形ABCD中,∠B=60°,E、F分别是AB、BC的中点,AF、CE相交于点O,则∠AOC=120°.