题目内容
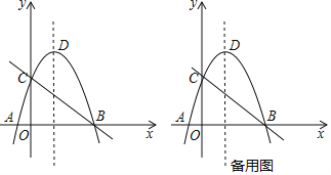
【题目】如图![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() ,点
,点![]() ,点
,点![]() 在
在![]() 轴上.
轴上.
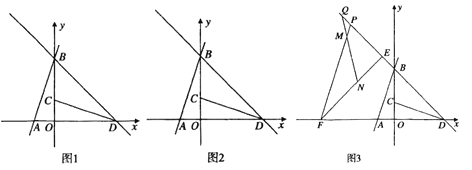
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 是直线
是直线![]() 在第二象限内一点,直线
在第二象限内一点,直线![]() 交
交![]() 轴于点
轴于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的解析式;
的解析式;
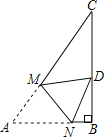
(3)如图![]() ,在(2)的条件下,
,在(2)的条件下,![]() 、
、![]() 是
是![]() 延长线上的两点(点
延长线上的两点(点![]() 在点
在点![]() 的右侧),
的右侧),![]() ,连接
,连接![]() ,
,![]() 是
是![]() 上一点,直线
上一点,直线![]() 交
交![]() 于点
于点![]() ,
,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
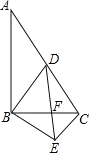
(1)现根据题意确定B,D的坐标,然后用待定系数法即可求解;(2)过点![]() 作
作![]() 于点
于点![]() .由(1)可知
.由(1)可知![]() .可得△EDF是等腰直角三角形.即
.可得△EDF是等腰直角三角形.即![]() .然后根据题意确定E的坐标和EH的表达式,然后看图写出四边形ABEF的面积表达式;(3)过点
.然后根据题意确定E的坐标和EH的表达式,然后看图写出四边形ABEF的面积表达式;(3)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,在
,在![]() 延长线上截取
延长线上截取![]() ,连接
,连接![]() ,然后说明四边形
,然后说明四边形![]() 是平行四边形,四边形
是平行四边形,四边形![]() 是正方形以及
是正方形以及![]() ,最后运用勾股定理完成解答.
,最后运用勾股定理完成解答.
解:(1)∵![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,∴
,∴![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .∵
.∵![]() ,
,![]() ,∴
,∴![]() .
.
∴![]() .∴
.∴![]() .设直线
.设直线![]() 的解析式为
的解析式为![]() ,把
,把![]() ,
,![]() 代入,解得
代入,解得![]() ,
,![]() .∴
.∴![]() .
.

(2)过点![]() 作
作![]() 于点
于点![]() .由(1)可知
.由(1)可知![]() .
.
∴△EDF是等腰直角三角形.
∴![]() .
.
由题意知![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.

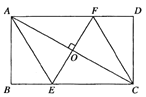
(3)如图,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,在
,在![]() 延长线上截取
延长线上截取![]() ,连接
,连接![]() .∵
.∵![]() ,∴
,∴![]() .∵
.∵![]() ,
,![]() ,∴四边形
,∴四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() .∴
.∴![]() .∴
.∴![]() .易得
.易得![]() ,∴
,∴![]() .∴易证四边形
.∴易证四边形![]() 是正方形.∴
是正方形.∴![]() .∴
.∴![]() .∴
.∴![]() ,
,![]() .∵
.∵![]() ,∴
,∴![]() .∴
.∴![]() .设
.设![]() ,则
,则![]() .∵
.∵![]() ,∴
,∴![]() .
.
∴在![]() 中,由勾股定理得
中,由勾股定理得![]() ,解得
,解得![]() ,
,![]() (舍去).∴
(舍去).∴![]() .∴
.∴![]() .∴
.∴![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目