题目内容
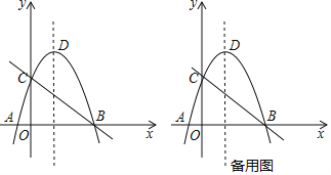
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,抛物线
两点,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴另一交点为
轴另一交点为![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式;
(2)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,求
的值最小,求![]() 的最小值;
的最小值;
(3)在抛物线的对称轴上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
由于抛物线的解析式中只有两个待定系数,因此将B、C两点的坐标代入抛物线中即可求出抛物线的解析式.
作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,则此时
,则此时![]() 为最小,再将
为最小,再将![]() 的坐标代入一次函数表达式即可解得
的坐标代入一次函数表达式即可解得
分别求出点P在x轴的位置即可.
解:(1)直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,则点
两点,则点![]() 的坐标分别为
的坐标分别为![]() ,
,
将点![]() 的坐标代入二次函数表达式得:
的坐标代入二次函数表达式得:![]() ,解得:
,解得:![]() ,
,
故函数的表达式为:![]() ,
,
令![]() ,则
,则![]() 或3,故点
或3,故点![]() ;
;
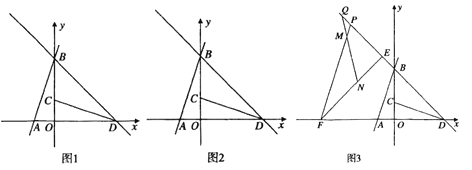
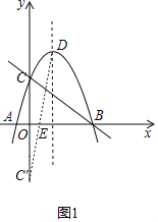
(2)如图1,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() 交
交![]() 轴于点
轴于点![]() ,则此时
,则此时![]() 为最小,
为最小,
函数顶点坐标为![]() ,点
,点![]() ,
,
将![]() 的坐标代入一次函数表达式并解得:
的坐标代入一次函数表达式并解得:
直线![]() 的表达式为:
的表达式为:![]() ,
,
当![]() 时,
时,![]() ,
,
故点![]() ;
;
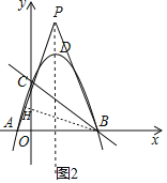
(3)①当点![]() 在
在![]() 轴上方时,如下图2,
轴上方时,如下图2,
∵![]() ,则
,则![]() ,
,
过点![]() 作
作![]() ,设
,设![]() ,
,
则![]() ,
,
由勾股定理得:![]() ,
,
![]() ,解得:
,解得:![]() (负值已舍去),
(负值已舍去),
则![]() ,
,
则![]() ;
;
②当点![]() 在
在![]() 轴下方时,
轴下方时,
则![]() ;
;
故点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目