题目内容
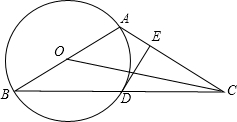 如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点.过点D作DE⊥AC交AC边于点E.
如图,以△ABC的一边AB为直径作⊙O,⊙O与BC边的交点D恰好为BC的中点.过点D作DE⊥AC交AC边于点E.(1)求证:DE是⊙O的切线;
(2)若∠ABC=30°,求tan∠BCO的值.
分析:(1)连接OD,根据三角形的中位线定理可求出OD∥AC,根据切线的性质可证明DE⊥OD,进而得证.
(2)过O作OF⊥BD,根据等腰三角形的性质及三角函数的定义用OB表示出OF、CF的长,根据三角函数的定义求解.
(2)过O作OF⊥BD,根据等腰三角形的性质及三角函数的定义用OB表示出OF、CF的长,根据三角函数的定义求解.
解答: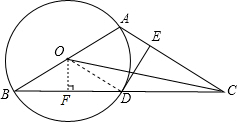 (1)证明:连接OD.
(1)证明:连接OD.
∵O为AB中点,D为BC中点,
∴OD∥AC.
∵DE为⊙O的切线,
∴DE⊥OD.
∴DE⊥AC.
(2)解:过O作OF⊥BD,则BF=FD.
在Rt△BFO中,∠B=30°,
∴OF=
OB,BF=
OB.
∵BD=DC,BF=FD,
∴FC=3BF=
OB.
在Rt△OFC中,
tan∠BCO=
=
=
=
.
 (1)证明:连接OD.
(1)证明:连接OD.∵O为AB中点,D为BC中点,
∴OD∥AC.
∵DE为⊙O的切线,
∴DE⊥OD.
∴DE⊥AC.
(2)解:过O作OF⊥BD,则BF=FD.
在Rt△BFO中,∠B=30°,
∴OF=
| 1 |
| 2 |
| ||
| 2 |
∵BD=DC,BF=FD,
∴FC=3BF=
3
| ||
| 2 |
在Rt△OFC中,
tan∠BCO=
| FO |
| FC |
| ||||
|
| 1 | ||
3
|
| ||
| 9 |
点评:此题主要考查了三角形中位线定理及切线的性质与判定、三角函数的定义等知识点,有一定的综合性,根据已知得出OF=
OB,BF=
OB,FC=3BF=
OB是解题关键.
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
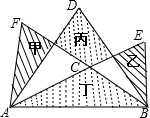 如图,以△ABC的每一条边为边作三个正三角形△ABD、△BCE和△ACF.已知这三个正三角形构成的图形中,甲、乙阴影部分的面积和等于丙、丁阴影部分的面积和,则∠FCE=( )
如图,以△ABC的每一条边为边作三个正三角形△ABD、△BCE和△ACF.已知这三个正三角形构成的图形中,甲、乙阴影部分的面积和等于丙、丁阴影部分的面积和,则∠FCE=( )| A、130° | B、140° | C、150° | D、160° |
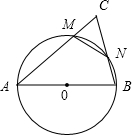 如图,以△ABC的边AB为直径画圆,与边AC交于M,与边BC交于N,已知△ABC的面积是△CMN面积的4倍,△ABC中有一个内角度数是另一内角度数的2倍,试计算△ABC三个内角的度数:
如图,以△ABC的边AB为直径画圆,与边AC交于M,与边BC交于N,已知△ABC的面积是△CMN面积的4倍,△ABC中有一个内角度数是另一内角度数的2倍,试计算△ABC三个内角的度数: 14、已知:如图分别以△ABC的每一条边,在三角形外作等边三角形,△ABD、△BCE、△ACF,则CD=AE=BF.(
14、已知:如图分别以△ABC的每一条边,在三角形外作等边三角形,△ABD、△BCE、△ACF,则CD=AE=BF.(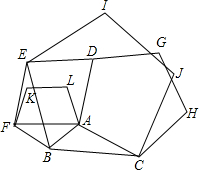 (2012•拱墅区一模)如图,以△ABC的各边为边,在BC的同侧分别作三个正五边形.它们分别是正五边形ABFKL、BCJIE、ACHGD,试探究:
(2012•拱墅区一模)如图,以△ABC的各边为边,在BC的同侧分别作三个正五边形.它们分别是正五边形ABFKL、BCJIE、ACHGD,试探究: 如图,以△ABC的任意两边为平行四边形的一组邻边,第三边为平行四边形的一条对角线,作出所有的平行四边形.
如图,以△ABC的任意两边为平行四边形的一组邻边,第三边为平行四边形的一条对角线,作出所有的平行四边形.