题目内容
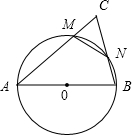如图，以△ABC的边AB为直径画圆，与边AC交于M，与边BC交于N，已知△ABC的面积是△CMN面积的4倍，△ABC中有一个内角度数是另一内角度数的2倍，试计算△ABC三个内角的度数：分析：连接BM，由圆内接四边形的性质可知，∠CNM=∠CAB=∠CAB，可证△CNM∽△CAB，又△ABC的面积是△CMN面积的4倍，可知相似比
=
，而AB为直径，∠BMC=90°，则∠C=60°，∠A+∠B=120°，由∠A=2∠B或∠B=2∠A，分类求解．
| CM |
| CB |
| 1 |
| 2 |
解答：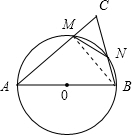
解：如图：连接BM，由圆内接四边形的性质可知，∠CNM=∠CAB，∠CMN=∠CBA，
∴△CNM∽△CAB，又△ABC的面积是△CMN面积的4倍，可知相似比
=
，
AB为直径，∠BMC=90°，
则∠C=60°，∠A+∠B=120°，
由∠A=2∠B或∠B=2∠A可得△ABC三个内角的度数，
∠A=80°，∠B=40°，∠C=60°或∠A=40°，∠B=80°，∠C=60°．
解：如图：连接BM，由圆内接四边形的性质可知，∠CNM=∠CAB，∠CMN=∠CBA，∴△CNM∽△CAB，又△ABC的面积是△CMN面积的4倍，可知相似比
| CM |
| CB |
| 1 |
| 2 |
AB为直径，∠BMC=90°，
则∠C=60°，∠A+∠B=120°，
由∠A=2∠B或∠B=2∠A可得△ABC三个内角的度数，
∠A=80°，∠B=40°，∠C=60°或∠A=40°，∠B=80°，∠C=60°．
点评：本题主要涉及圆内接四边形的性质，相似三角形的判定与性质，相似比与面积比的关系．
练习册系列答案
相关题目
26、如图，以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE，四边形ADFE是平行四边形．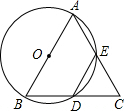
如图，以△ABC的边AB为直径作⊙O，交BC于D点，交AC于E点，BD=DE
（2011•峨眉山市二模）如图，以△ABC的边AB为直径作⊙O，BC与⊙O交于D，D是BC的中点，过D作DE⊥AC，交AC于点E．
（2010•黔东南州）如图，以△ABC的边BC为直径作⊙O分别交AB，AC于点F．点E，AD⊥BC于D，AD交于⊙O于M，交BE于H．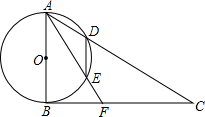
如图，以△ABC的边AB为直径的⊙O交AC于点D，弦DE∥AB，∠C=∠BAF