Question

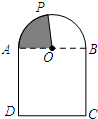
如图是一个由正方形ABCD和半圆O组成的封闭图形，点O是圆心．点P从点A出发，沿弧AB，线段BC和线段CD，线段DA匀速运动，到达终点A．运动过程中OP扫过的面积（S）随时间（t）变化的图象大致是（ ）

A．
B．
C．
D．

Answer 1

【答案】分析：解决本题的关键是读懂图意，根据题意写出各段的解析式，由此可得出答案．
解答：解：∵设正方形的边长为1，则半圆的半径为0.5；设点P的运动速度为a，时间为t，
当点P从点A到点B的过程中，OP扫过的面积S=at×0.5=at；
当点P在线段BC上运动时，OP所扫过的面积=S_△BOP+S_半圆=×0.5×（at-π）+π×（）²=at；
当点P在线段CD上时，OP所扫过的面积=S_△OBC+S_半圆+S_△OCP=×1×+π×（）²+×1×（at-1-π）=at-；
当点P在线段AD上时，OP所扫过的面积=S_△OBC+S_半圆+S_△OCD+S_△OPD=×1×+π×（）²+×1×1+××（at-2-π）=at+．
∴动过程中OP扫过的面积（S）随时间（t）变化的图象是正比例函数和一次函数组合．
故选A．
点评：本题考查了动点问题的函数图象：先根据几何性质得到与动点有关的两变量之间的函数关系，然后利用函数解析式和函数性质画出其函数图象，注意自变量的取值范围．