题目内容
在平行四边形的边AB和AD上分别取点E和F，使AE=| 1 |
| 3 |
| 1 |
| 4 |
| AG |
| AC |
| 1 |
| 7 |
| 1 |
| 7 |
分析：根据题意在AD上截取AH=
AD，得到AG与OC的关系，然后由相似三角形得到OC与AO的关系，代入
求出比值．
| 3 |
| 4 |
| AG |
| AC |
解答：
解：如图，在AD上取点H，使AH=
AD，连接BH交AC于O，
则
=
，即AG=
AO，
又△AOH∽△COB，所以
=
=
，CO=
AO，
所以
=
=
=
=
．
故答案为：
．
解：如图，在AD上取点H，使AH=| 3 |
| 4 |
则
| AG |
| AO |
| 1 |
| 3 |
| 1 |
| 3 |
又△AOH∽△COB，所以
| AO |
| CO |
| AH |
| CB |
| 3 |
| 4 |
| 4 |
| 3 |
所以
| AG |
| AC |
| AG |
| AO+CO |
| ||
AO+
|
| ||
|
| 1 |
| 7 |
故答案为：
| 1 |
| 7 |
点评：本题考查了相似三角形的判定与性质以及平行四边形的性质，解题的关键是构造相似三角形，利用相似三角形的对应边的比相等进行转换．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
相关题目
在平行四边形的边AB和AD上分别取点E和F，使AE=
AB，AF=
AD，连接EF交对角线AC于G，则
的值是________．
AB，AF=
AD，连接EF交对角线AC于G，则
的值是 ．
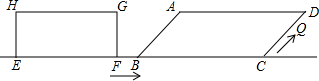
，点EFBC在同一直线上，且FB=1cm，矩形从F点开始以1cm/s的速度沿直线FC向右移动，当D点落在边CF所在直线上即停止．