题目内容
4. 本市新建一座圆形人工湖,为测量该湖的半径,小杰和小丽沿湖边选取A,B,C三根木柱,使得A,B之间的距离与A,C之间的距离相等,并测得BC长为120米,A到BC的距离为4米,如图所示.
本市新建一座圆形人工湖,为测量该湖的半径,小杰和小丽沿湖边选取A,B,C三根木柱,使得A,B之间的距离与A,C之间的距离相等,并测得BC长为120米,A到BC的距离为4米,如图所示.(1)请你帮他们求出该湖的半径;
(2)如果在圆周上再另取一点P,建造一座连接B,C,P三点的三角形艺术桥,且△BCP为直角三角形,问:这样的P点可以有几处?如何找到?
分析 (1)设圆心为点O,连接OB,OA,AB=AC,得出$\widehat{AB}$=$\widehat{AC}$,再根据等弦对等弧,得出点A是弧BC的中点.结合垂径定理的推论,知OA垂直平分弦,设圆的半径,结合垂径定理和勾股定理列出关于半径的方程,即可求得圆的半径;
(2)根据垂直的定义即可得到结论.
解答  解:设圆心为点O,连接OB,OA,OA交线段BC于点D,
解:设圆心为点O,连接OB,OA,OA交线段BC于点D,
∵AB=AC,
∴$\widehat{AB}$=$\widehat{AC}$,
∴OA⊥BC,
∴BD=DC=$\frac{1}{2}$BC=60
∵DA=4米,
在Rt△BDO中,OB2=OD2+BD2,
设OB=x米,
则x2=(x-4)2+602,
解得x=452.
∴人工湖的半径为452米;
(2)这样的P点可以有2处,过点B或点C作BC的垂线交圆于一点,此点即为P点.
点评 此题考查了垂径定理的应用,用到的知识点是等弦对等弧、垂径定理的推论、勾股定理,关键是根据题意作出辅助线,构造直角三角形.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
16.如果设5a=m,5b=n,那么5a-b等于( )
| A. | m+n | B. | mn | C. | m-n | D. | $\frac{m}{n}$ |
13.下列实数中,是无理数的为( )
| A. | -3.567 | B. | 0.101001 | C. | $\sqrt{2}$ | D. | $\frac{1}{3}$ |
 根据下列语句画出图形.
根据下列语句画出图形.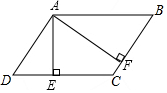 如图,在平行四边形ABCD中,AE⊥CD,垂足为E,AF⊥BC,垂足为F,AD=4,BF=3,∠EAF=60°,设$\overrightarrow{AB}$=$\overrightarrow{a}$,如果向量$\overrightarrow{CE}$=k$\overrightarrow{a}$(k≠0),那么k的值是-$\frac{2}{3}$.
如图,在平行四边形ABCD中,AE⊥CD,垂足为E,AF⊥BC,垂足为F,AD=4,BF=3,∠EAF=60°,设$\overrightarrow{AB}$=$\overrightarrow{a}$,如果向量$\overrightarrow{CE}$=k$\overrightarrow{a}$(k≠0),那么k的值是-$\frac{2}{3}$.