题目内容
13.对抛物线y=-2x2+4x-3而言,下列结论正确的是( )| A. | 与x轴有两个交点 | B. | 开口向上 | ||
| C. | 与x轴的交点坐标是(0,3) | D. | 顶点坐标是(1,-1) |
分析 根据△的符号,可判断图象与x轴的交点情况,根据二次项系数可判断开口方向,令函数式中x=0,可求图象与y轴的交点坐标,利用配方法可求图象的顶点坐标.
解答 解:A、∵△=42-4×(-2)×(-3)=-8<0,抛物线与x轴无交点,本选项错误;
B、∵二次项系数-2<0,抛物线开口向下,本选项错误;
C、当x=0时,y=-3,抛物线与y轴交点坐标为(0,-3),本选项错误;
D、∵y=-2x2+4x-3=-2(x-1)2-1,∴抛物线顶点坐标为(1,-1),本选项正确.
故选D
点评 本题考查了抛物线的性质与解析式的关系.关键是明确抛物线解析式各项系数与性质的联系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.用四舍五入的方法将3.602精确到0.01的结果是( )
| A. | 3.6 | B. | 3.60 | C. | 3.602 | D. | 3.61 |
2.某公司一周内货物进出的吨数记录如下表(“+”表示进库,“-”表示出库)
(1)若周六结束时仓库内还有货物420吨,则周日开始时,仓库内有货物多少吨?
(2)如果该仓库货物进出的装卸都是每吨5元,那么这一周内共需付多少元装卸费?
| 日期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 进出的吨数 | +20 | -25 | -16 | +32 | -24 | -20 | -16 |
(2)如果该仓库货物进出的装卸都是每吨5元,那么这一周内共需付多少元装卸费?
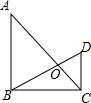 将一副三角板按图叠放,∠A=45°,∠D=60°,∠ABC=∠DCB=90°,则△AOB与△DOC的面积之比为3:1.
将一副三角板按图叠放,∠A=45°,∠D=60°,∠ABC=∠DCB=90°,则△AOB与△DOC的面积之比为3:1.