题目内容
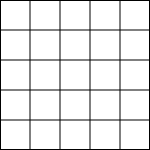 如图,点A是5×5的正方形网格的顶点(即横线与竖线的交点)已知每个小正方形的边长为1,请你在给定的网格中按下列要求画出图形,并解决问题
如图,点A是5×5的正方形网格的顶点(即横线与竖线的交点)已知每个小正方形的边长为1,请你在给定的网格中按下列要求画出图形,并解决问题(1)从点A出发画一条线段AB,使它的另一个端点B在格点上,且长度为
| 20 |
(2)再从点B出发画一条线段BC,使它的另一个端点C在格点上,且长度为
| 8 |
(3)连接AC,则S△ABC=
6
6
(请用铅笔画图)分析:(1)根据20=22+42,则B点与A点相差横2竖4即可,可画出AB线段如图;
(2)根据8=22+22,则B点与C点相差横2竖2即可,可画出BC线段如图;
(3)根据BC、AC的长度断定△ABC是等腰三角形,然后由等腰三角形“三合一”的性质作辅助线BC边上的中线AD,根据勾股定理求得AD的长度;最后由三角形的面积公式来求△ABC的面积即可.
(2)根据8=22+22,则B点与C点相差横2竖2即可,可画出BC线段如图;
(3)根据BC、AC的长度断定△ABC是等腰三角形,然后由等腰三角形“三合一”的性质作辅助线BC边上的中线AD,根据勾股定理求得AD的长度;最后由三角形的面积公式来求△ABC的面积即可.
解答: 解:(1)图示线段AB长为:
解:(1)图示线段AB长为:
=
;
(2)图示线段BC长为:
=
;
(3)根据图示知,AB=AC=
.
过点A作BC边上的中线AD交BC于点D,则AD⊥BC,
∵由勾股定理知AD=
=3
,
∴S△ABC=
BC•AD=
×
×3
=6.
故答案是:6.
 解:(1)图示线段AB长为:
解:(1)图示线段AB长为:| 42+22 |
| 20 |
(2)图示线段BC长为:
| 22+22 |
| 8 |
(3)根据图示知,AB=AC=
| 20 |
过点A作BC边上的中线AD交BC于点D,则AD⊥BC,
∵由勾股定理知AD=
| 32+32 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 2 |
故答案是:6.
点评:本题考查了勾股定理.如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 函数y=
函数y= 如图,点D是⊙O直径CA的延长线上一点,点B在⊙O上,且AB=AD=AO.
如图,点D是⊙O直径CA的延长线上一点,点B在⊙O上,且AB=AD=AO. 如图,点G是正方形ABCD的边CD上的一点(不包括点C、D).
如图,点G是正方形ABCD的边CD上的一点(不包括点C、D). 如图,点E是正方形ABCD的边BC上的一点,∠DAE的平分线AF交BC的延长线于点F,交CD于点G
如图,点E是正方形ABCD的边BC上的一点,∠DAE的平分线AF交BC的延长线于点F,交CD于点G 已知:如图,点C是线段AB的中点,点D是线段BC的中点,AB=20cm,那么线段AD等于( )
已知:如图,点C是线段AB的中点,点D是线段BC的中点,AB=20cm,那么线段AD等于( )