Question

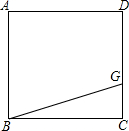如图，点G是正方形ABCD的边CD上的一点（不包括点C、D）．
（1）将△CBG绕点C按顺时针方向旋转90°，请你在图中画出旋转后的图形；
（2）观察图形，猜想BG与其对应线段之间的关系，并证明你的结论．

Answer 1

分析：（1）在BC延长线上截取CG′=CG，然后连接DG′，△CDG′即为旋转后的图形；
（2）根据旋转的性质可得△CDG′和△CBG全等，再根据全等三角形对应边相等可得BG=DG′，∠CBG=∠CDG′，然后求出∠CBG+∠G′=90°，设BG的延长线于DG′相交于H，再求出∠BHG′=90°，然后根据垂线的定义解答．

解答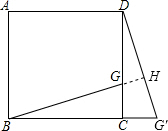：解：（1）△CDG′如图所示；

（2）BG=DG′，BG⊥DG′．
证明如下：由旋转的性质，△CDG′≌△CBG，
∴BG=DG′，∠CBG=∠CDG′，
∵∠CDG′+∠G′=180°-90°=90°，
∴∠CBG+∠G′=90°，
设BG的延长线于DG′相交于H，
在△BCH中，∠BHG′=180°-（∠CBG+∠G′）=180°-90°=90°．

点评：本题考查了利用旋转变换作图，正方形的性质，熟练掌握旋转和正方形的性质是解题的关键．