Question

【题目】如图，在△ABC中，已知于点D，AE平分

（1）试探究与的关系；

（2）若F是AE上一动点，当F移动到AE之间的位置时，,如图2所示，此时的关系如何？

（3）若F是AE上一动点，当F继续移动到AE的延长线上时，如图3，，①中的结论是否还成立？如果成立请说明理由，如果不成立，写出新的结论.

Answer 1

【答案】（1）∠EAD=（∠C-∠B），理由见解析；
（2）∠EFD=（∠C-∠B），理由见解析；

（3）∠AFD=（∠C-∠B）成立，理由见解析.

【解析】

（1）由图不难发现∠EAD=∠EAC-∠DAC，再根据三角形的内角和定理结合角平分线的定义分别用结论中出现的角替换∠EAC和∠DAC；
（2）作于G转化为（1）中的情况，利用（1）的结论即可解决；

（3）作于H转化为（1）中的情况，利用（1）的结论即可解决．

解：（1）∠EAD=（∠C-∠B）.理由如下：

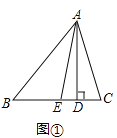
∵AE平分∠BAC，
∴∠BAE=∠CAE=∠BAC
∵∠BAC=180°-（∠B+∠C）
∴∠EAC= [180°-（∠B+∠C）]
∵AD⊥BC，
∴∠ADC=90°，
∴∠DAC=180°-∠ADC-∠C=90°-∠C，
∵∠EAD=∠EAC-∠DAC
∴∠EAD= [180°-（∠B+∠C）]-（90°-∠C）=（∠C-∠B）．
（2）∠EFD=（∠C-∠B）.理由如下：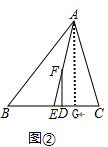

作于G

由（1）可知∠EAG=（∠C-∠B）

∵，
∴FD∥AG
∴∠EAG=∠EFD

∴∠EFD=（∠C-∠B）
（3）∠AFD=（∠C-∠B）．理由如下：

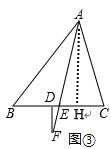
作于H

由（1）可知∠EAH=（∠C-∠B）

∵，
∴FD∥AH
∴∠EAH=∠AFD

∴∠AFD=（∠C-∠B）