题目内容
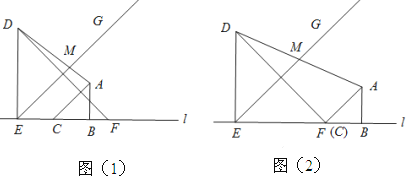
【题目】如图1,两个等腰直角三角板![]() 和
和![]() 有一条边在同一条直线
有一条边在同一条直线![]() 上,
上, ![]() ,
, ![]() .将射线
.将射线![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,交直线
,交直线![]() 于点
于点![]() .将图1中的三角板
.将图1中的三角板![]() 沿直线
沿直线![]() 向右平移,设
向右平移,设![]() 、
、![]() 两点间的距离为
两点间的距离为![]() .
.
解答问题:
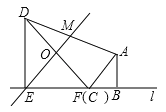
(1)①当点![]() 与点
与点![]() 重合时,如图2所示,可得
重合时,如图2所示,可得![]() 的值为 ;
的值为 ;
②在平移过程中, ![]() 的值为 (用含
的值为 (用含![]() 的代数式表示);
的代数式表示);
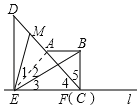
(2)将图2中的三角板![]() 绕点
绕点![]() 逆时针旋转,原题中的其他条件保持不变.当点
逆时针旋转,原题中的其他条件保持不变.当点![]() 落在线段
落在线段![]() 上时,如图3所示,计算
上时,如图3所示,计算![]() 的值;
的值;
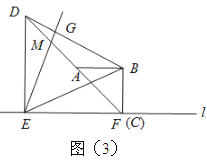
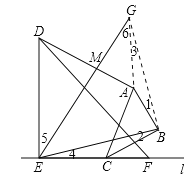
(3)将图1中的三角板ABC绕点C逆时针旋转![]() 度,
度, ![]() ≤
≤![]() ,原题中的其他条件保持不变.如图4所示,请补全图形,计算
,原题中的其他条件保持不变.如图4所示,请补全图形,计算![]() 的值(用含k的代数式表示).
的值(用含k的代数式表示).

【答案】(1)①1, ②![]() ;(2)1;(3)
;(2)1;(3)![]() .
.
【解析】试题分析:(1)①根据题意可得EM垂直平分DF,直线AF∥EM,从而![]() 转化为
转化为![]() ,继而得出结论;②仿照①的思路进行求解即可;
,继而得出结论;②仿照①的思路进行求解即可;
(2)先补全图形,连接AE,分别求出AM及DM的值,然后可确定比值.
(3)先画出图形,然后证明△ABG≌△CBE,继而推出AG∥DE,△AGM∽△DEM,利用相似三角形的性质即可得出答案.
试题解析:解:(1)①如图,∵∠MEB=45°,∠AFB=45°,∴EM垂直且平分DF,AF∥EM,∴ ![]() =
=![]() =1;
=1;
②如图:
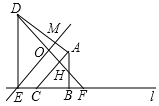
由①可得![]() =
=![]() ;
;
(2)连接AE.∵△ABC,△DEF均为等腰直角三角形,DE=2,AB=1,∴EF=2,BC=1,∠DEF=90°,∠4=∠5=45°,∴DF=![]() ,AC=
,AC=![]() ,∠EFB=90°,∴DF=2AC,AD=
,∠EFB=90°,∴DF=2AC,AD=![]() ,∴点A为CD的中点,∴EA⊥DF,EA平分∠DEF,∴∠MAE=90°,∠AEF=45°,AE=
,∴点A为CD的中点,∴EA⊥DF,EA平分∠DEF,∴∠MAE=90°,∠AEF=45°,AE=![]() .∵∠BEM=45°,∴∠1+∠2=∠3+∠2=45°,∴∠1=∠3,∴△AEM∽△FEB,∴
.∵∠BEM=45°,∴∠1+∠2=∠3+∠2=45°,∴∠1=∠3,∴△AEM∽△FEB,∴![]() ,∴AM=
,∴AM=![]() ,∴DM=AD﹣AM=
,∴DM=AD﹣AM=![]() ,∴
,∴![]() =1.
=1.
(3)过B作BE的垂线交直线EM于点G,连接AG、BG,∴∠EBG=90°.∵∠BEM=45°,∴∠EGB=∠BEM=45°,∴BE=BG.∵△ABC为等腰直角三角形,∴BA=BC,∠ABC=90°,∴∠1=∠2,∴△ABG≌△CBE,∴AG=EC=k,∠3=∠4.∵∠3+∠6=∠5+∠4=45°,∴∠6=∠5,∴AG∥DE,∴△AGM∽△DEM,∴ ![]() .
.

 阅读快车系列答案
阅读快车系列答案