题目内容
1．
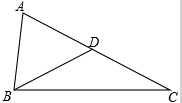如图，在△ABC中，∠C=29°，D为AC上一点，且AB=AD，DB=DC．求∠A的度数．
分析 根据等腰三角形的性质得到∠DBC=∠C=29°，由外角的性质得到∠ADB=∠C+∠DBC=58°，由于AB=AD，于是得到∠ABD=∠ADB=58°，然后根据三角形的内角和即可得到结论．
解答 解：∵DB=DC，∠C=29°，
∴∠DBC=∠C=29°，
∴∠ADB=∠C+∠DBC=58°，
∵AB=AD，
∴∠ABD=∠ADB=58°，
∴∠A=180°-∠ABD-∠ADB=64°．
点评 本题考查了等腰三角形的性质及三角形内角和为180°等知识．此类已知三角形边之间的关系求角的度数的题，一般是利用等腰（等边）三角形的性质得出有关角的度数，进而求出所求角的度数．
练习册系列答案
相关题目
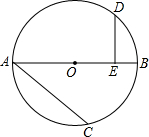如图，已知AB为⊙O的直径，D、C为⊙O上两点，弧AD=弧DC，连结AC．过点D作DE⊥0B于E．求证：DE=$\frac{1}{2}$AC．
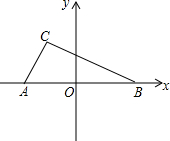在△ABC中，∠ACB=90°，∠BAC=60°，AC=2，如图，以AB所在的直线为x轴，以AB的垂直平分线为y轴，建立直角坐标系，求点A、B、C的坐标．