题目内容
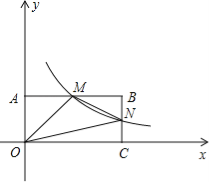
【题目】在等边△ABC外侧作直线AM,点C关于AM的对称点为D,连接BD交AM于点E,连接CE,CD,AD.
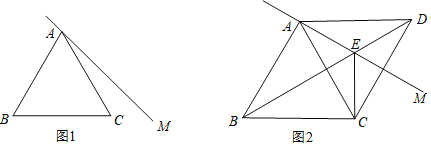
(1)依题意补全图1,并求∠BEC的度数;
(2)如图2,当∠MAC=30°时,判断线段BE与DE之间的数量关系,并加以证明;
(3)若0°<∠MAC<120°,当线段DE=2BE时,直接写出∠MAC的度数.
【答案】(1)补全图形如图1所示,见解析,∠BEC=60°;(2)BE=2DE,见解析;(3)∠MAC=90°.
【解析】
(1)根据轴对称作出图形,先判断出∠ABD=∠ADB=y,再利用三角形的内角和得出x+y即可得出结论;
(2)同(1)的方法判断出四边形ABCD是菱形,进而得出∠CBD=30°,进而得出∠BCD=90°,即可得出结论;
(3)先作出EF=2BE,进而判断出EF=CE,再判断出∠CBE=90°,进而得出∠BCE=30°,得出∠AEC=60°,即可得出结论.
(1)补全图形如图1所示,
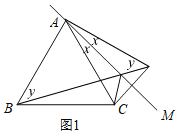
根据轴对称得,AD=AC,∠DAE=∠CAE=x,∠DEM=∠CEM.
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°.
∴AB=AD.
∴∠ABD=∠ADB=y.
在△ABD中,2x+2y+60°=180°,
∴x+y=60°.
∴∠DEM=∠CEM=x+y=60°.
∴∠BEC=60°;
(2)BE=2DE,
证明:∵△ABC是等边三角形,
∴AB=BC=AC,
由对称知,AD=AC,∠CAD=2∠CAM=60°,
∴△ACD是等边三角形,
∴CD=AD,
∴AB=BC=CD=AD,
∴四边形ABCD是菱形,且∠BAD=2∠CAD=120°,
∴∠ABC=60°,
∴∠ABD=∠DBC=30°,
由(1)知,∠BEC=60°,
∴∠ECB=90°.
∴BE=2CE.
∵CE=DE,
∴BE=2DE.
(3)如图3,(本身点C,A,D在同一条直线上,为了说明∠CBD=90°,画图时,没画在一条直线上)
延长EB至F使BE=BF,
∴EF=2BE,
由轴对称得,DE=CE,
∵DE=2BE,
∴CE=2BE,
∴EF=CE,
连接CF,同(1)的方法得,∠BEC=60°,
∴△CEF是等边三角形,
∵BE=BF,
∴∠CBE=90°,
∴∠BCE=30°,
∴∠ACE=30°,
∵∠AED=∠AEC,∠BEC=60°,
∴∠AEC=60°,
∴∠MAC=180°﹣∠AEC﹣∠ACE=90°.


【题目】同学们设计了一个重复抛掷的实验:全班48人分为8个小组,每组抛掷同一型号的一枚瓶盖300次,并记录盖面朝上的次数,下表是依次累计各小组的实验结果.
1组 | 1~2组 | 1~3组 | 1~4组 | 1~5组 | 1~6组 | 1~7组 | 1~8组 | |
盖面朝上次数 | 165 | 335 | 483 | 632 | 801 | 949 | 1122 | 1276 |
盖面朝上频率 | 0.550 | 0.558 | 0.537 | 0.527 | 0.534 | 0.527 | 0.534 | 0.532 |
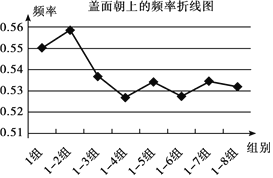
根据实验,你认为这一型号的瓶盖盖面朝上的概率为____,理由是:____.