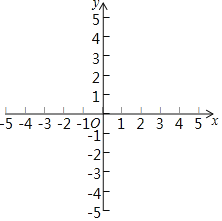题目内容
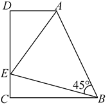
【题目】如图,在![]() 中,AB=AC,
中,AB=AC,![]() ,点D是BC的中点,DE⊥AB于点E,DF⊥AC于点F.
,点D是BC的中点,DE⊥AB于点E,DF⊥AC于点F.

(1)∠EDB=_____![]() (用含
(用含![]() 的式子表示)
的式子表示)
(2)作射线DM与边AB交于点M,射线DM绕点D顺时针旋转![]() ,与AC边交于点N.
,与AC边交于点N.
①根据条件补全图形;
②写出DM与DN的数量关系并证明;
③用等式表示线段BM、CN与BC之间的数量关系,(用含![]() 的锐角三角函数表示)并写出解题思路.
的锐角三角函数表示)并写出解题思路.
【答案】(1)![]() ;(2)(2)①见解析;②DM=DN,理由见解析;③数量关系:
;(2)(2)①见解析;②DM=DN,理由见解析;③数量关系:![]()
【解析】
(1)先利用等腰三角形的性质和三角形内角和得到∠B=∠C=90°﹣α,然后利用互余可得到∠EDB=α;
(2)①如图,利用∠EDF=180°﹣2α画图;
②先利用等腰三角形的性质得到DA平分∠BAC,再根据角平分线性质得到DE=DF,根据四边形内角和得到∠EDF=180°﹣2α,所以∠MDE=∠NDF,然后证明△MDE≌△NDF得到DM=DN;
③先由△MDE≌△NDF可得EM=FN,再证明△BDE≌△CDF得BE=CF,利用等量代换得到BM+CN=2BE,然后根据正弦定义得到BE=BDsinα,从而有BM+CN=BCsinα.
(1)∵AB=AC,∴∠B=∠C![]() (180°﹣∠A)=90°﹣α.
(180°﹣∠A)=90°﹣α.
∵DE⊥AB,∴∠DEB=90°,∴∠EDB=90°﹣∠B=90°﹣(90°﹣α)=α.
故答案为:α;
(2)①如图:
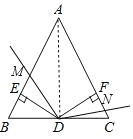
②DM=DN.理由如下:∵AB=AC,BD=DC,∴DA平分∠BAC.
∵DE⊥AB于点E,DF⊥AC于点F,∴DE=DF,∠MED=∠NFD=90°.
∵∠A=2α,∴∠EDF=180°﹣2α.
∵∠MDN=180°﹣2α,∴∠MDE=∠NDF.
在△MDE和△NDF中,∵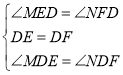 ,∴△MDE≌△NDF,∴DM=DN;
,∴△MDE≌△NDF,∴DM=DN;
③数量关系:BM+CN=BCsinα.
证明思路为:先由△MDE≌△NDF可得EM=FN,再证明△BDE≌△CDF得BE=CF,所以BM+CN=BE+EM+CF﹣FN=2BE,接着在Rt△BDE可得BE=BDsinα,从而有BM+CN=BCsinα.

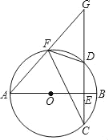
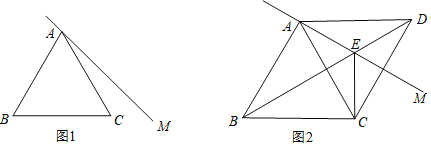
【题目】如图1,AB为半圆O的直径,半径的长为4cm,点C为半圆上一动点,过点C作CE⊥AB,垂足为点E,点D为弧AC的中点,连接DE,如果DE=2OE,求线段AE的长.
小何根据学习函数的经验,将此问题转化为函数问题解决.
小华假设AE的长度为xcm,线段DE的长度为ycm.
(当点C与点A重合时,AE的长度为0cm),对函数y随自变量x的变化而变化的规律进行探究.
下面是小何的探究过程,请补充完整:(说明:相关数据保留一位小数).
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 0 | 1.6 | 2.5 | 3.3 | 4.0 | 4.7 |
| 5.8 | 5.7 |
当x=6cm时,请你在图中帮助小何完成作图,并使用刻度尺度量此时线段DE的长度,填写在表格空白处:
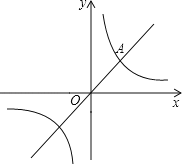
(2)在图2中建立平面直角坐标系,描出补全后的表中各组对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象解决问题,当DE=2OE时,AE的长度约为 cm.