题目内容
 如图,△ABE是边长为21的正三角形.已知四边形BCDE的周长是△ABE周长的两倍.则五边形ABCDE的周长是
如图,△ABE是边长为21的正三角形.已知四边形BCDE的周长是△ABE周长的两倍.则五边形ABCDE的周长是
- A.137
- B.147
- C.157
- D.167
B
分析:由△ABE是边长为21的正三角形,根据正三角形的性质,即可求得△ABE周长,又由四边形BCDE的周长是△ABE周长的两倍,求得四边形BCDE的周长,继而可得BC+CD+DE的长,则可求得五边形ABCDE的周长.
解答:∵△ABE是边长为21的正三角形,
∴△ABE周长为:AB+AE+BE=3×21=63,
∵四边形BCDE的周长是△ABE周长的两倍,
∴BC+CD+DE+BE=2×63=126,
∴BC+CD+DE=126-21=105,
∴五边形ABCDE的周长是:AB+BC+CD+DE+AE=(AB+AE)+(BC+CD+DE)=21+21+105=147.
故选B.
点评:此题考查了等边三角形的性质.此题难度不大,解题的关键是注意数形结合思想与整体思想的应用.
分析:由△ABE是边长为21的正三角形,根据正三角形的性质,即可求得△ABE周长,又由四边形BCDE的周长是△ABE周长的两倍,求得四边形BCDE的周长,继而可得BC+CD+DE的长,则可求得五边形ABCDE的周长.
解答:∵△ABE是边长为21的正三角形,
∴△ABE周长为:AB+AE+BE=3×21=63,
∵四边形BCDE的周长是△ABE周长的两倍,
∴BC+CD+DE+BE=2×63=126,
∴BC+CD+DE=126-21=105,
∴五边形ABCDE的周长是:AB+BC+CD+DE+AE=(AB+AE)+(BC+CD+DE)=21+21+105=147.
故选B.
点评:此题考查了等边三角形的性质.此题难度不大,解题的关键是注意数形结合思想与整体思想的应用.

练习册系列答案
相关题目
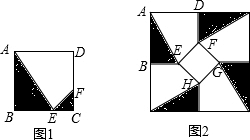 BC和CD上,若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形EFGH.
BC和CD上,若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形EFGH.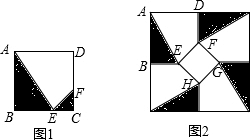 BC和CD上,若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形EFGH.
BC和CD上,若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分成四边形EFGH.
