题目内容
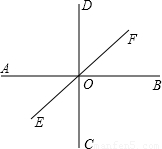
(2003•徐州)如图,直线AB⊥CD于O,直线EF过点O,且∠AOE=40°,则∠BOF= 度,∠DOF= 度.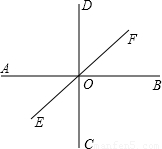
【答案】分析:已知∠AOE=40°,利用对顶角相等可求∠BOF;因为AB⊥CD,则∠DOF+∠BOF=90°,用互余关系求∠DOF.
解答:解:∵直线AB、EF相交于点O,
∴∠BOF=∠AOE=40°,
∵AB⊥CD,
∴∠DOF=90°-∠BOF
=90°-40°=50°.
点评:本题考查了垂直的定义和对顶角的性质,要注意领会由垂直得直角这一要点.
解答:解:∵直线AB、EF相交于点O,
∴∠BOF=∠AOE=40°,
∵AB⊥CD,
∴∠DOF=90°-∠BOF
=90°-40°=50°.
点评:本题考查了垂直的定义和对顶角的性质,要注意领会由垂直得直角这一要点.

练习册系列答案
相关题目