Question

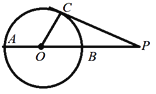
【题目】如图，已知直线l与⊙O相离，OA⊥l于点A，OA＝5，OA与⊙O相交于点P，AB与⊙O相切于点B，BP的延长线交直线l于点C.

(1)试判断线段AB与AC的数量关系，并说明理由；

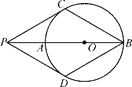
(2)若在⊙O上存在点Q，使△QAC是以AC为底边的等腰三角形，求⊙O的半径r的取值范围．

Answer 1

【答案】（1）AB＝AC（2）≤r<5

【解析】

（1）连接，根据切线的性质和垂直得出，推出，求出，根据等腰三角形的判定推出即可；

（2）根据已知得出在的垂直平分线上，作出线段的垂直平分线，作，求出，求出范围，再根据相离得出，即可得出答案.

(1)AB＝AC，理由如下：

如图1，连结OB.

∵AB切⊙O于B，OA⊥AC，

∴∠OBA＝∠OAC＝90°，

∴∠OBP＋∠ABP＝90°，∠ACP＋∠APC＝90°，

∵OP＝OB，

∴∠OBP＝∠OPB，

∵∠OPB＝∠APC，

∴∠ACP＝∠ABC，

∴AB＝AC；　

(2)如图2，作出线段AC的垂直平分线MN，作OE⊥MN，则可以推出；

又∵圆O与直线MN有交点，

∴，

，

，

r2≥5，

∴，

又∵圆O与直线l相离，

∴r<5，

即.

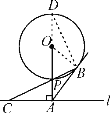
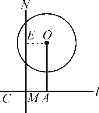
图1 2