Question

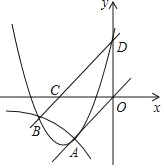
【题目】如图，已知正比例函数和反比例函数的图象都经过点A（﹣3，﹣3）．

（1）求正比例函数和反比例函数的表达式；

（2）把直线OA向上平移后与反比例函数的图象交于点B（﹣6，m），与x轴交于点C，求m的值和直线BC的表达式；

（3）在（2）的条件下，直线BC与y轴交于点D，求以点A，B，D为顶点的三角形的面积；

（4）在（3）的条件下，点A，B，D在二次函数的图象上，试判断该二次函数在第三象限内的图象上是否存在一点E，使四边形OECD的面积S1与四边形OABD的面积S满足：S1=S？若存在，求点E的坐标；若不存在，请说明理由．

Answer 1

【答案】（1） ，；（2） ,；（3）；（4）E的坐标是（﹣2，﹣）．

【解析】

（1）利用待定系数法即可求得函数的解析式；

（2）把B（﹣6，m）代入反比例函数解析式即可求出m的值，再根据直线平移的性质即可求直线BC的表达式；

（3）作AM⊥y轴于点M，作BN⊥y轴于点N，根据S四边形ABDM=S梯形ABNM+S△BDN，S△ABD=S四边形ABDM﹣S△ADM即可求解；

（4）设二次函数的解析式是y=ax2+bx+，然后利用待定系数法求得二次函数的解析式，根据S1=S即可求得S1的值，根据S1=S△OCD+S△OCE列方程求出y0的值，再由E（x0，y0）在二次函数的图象上，即可求得x0的值，进而求得E的坐标．

解：（1）设正比例函数的解析式是y=kx，代入（﹣3，﹣3），得：﹣3k=﹣3，解得：k=1，

则正比例函数的解析式是：y=x；

设反比例函数的解析式是y=，把（﹣3，﹣3）代入解析式得：k1=9，

则反比例函数的解析式是：y=；

（2）m==﹣，则点B的坐标是（﹣6，﹣），

∵y=k3x+b的图象是由y=x平移得到，

∴k3=1，即y=x+b，

故一次函数的解析式是：y=x+；

（3）∵y=x+的图象交y轴于点D，

∴D的坐标是（0，），

作AM⊥y轴于点M，作BN⊥y轴于点N．

∵A的坐标是（﹣3，﹣3），B的坐标是（6，﹣），

∴M的坐标是（0，﹣3），N的坐标是（0，﹣）．

∴OM=3，ON=．

则MD=3+=，DN=+=6，MN=3﹣=．

则S△ADM=×3×=，S△BDN=×6×6=18，S梯形ABNM=×（3+6）×=．

则S四边形ABDM=S梯形ABNM+S△BDN=+18=，

S△ABD=S四边形ABDM﹣S△ADM=﹣=；

（4）设二次函数的解析式是y=ax2+bx+，

则，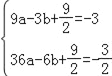

解得：，

则这个二次函数的解析式是：y=x2+4x+；

点C的坐标是（﹣，0）．

则S=×6﹣×6×6﹣×3×﹣×3×=45﹣18﹣﹣=．

假设存在点E（x0，y0），使S1=S=×=．

∵四边形CDOE的顶点E只能在x轴的下方，

∴y0＜0，

∴S1=S△OCD+S△OCE=××﹣×y0=﹣y0，

∴﹣y0=，

∴y0=﹣，

∵E（x0，y0）在二次函数的图象上，

∴x02+4x0+=﹣，

解得：x0=﹣2或﹣6．

当x0=﹣6时，点E（﹣6，﹣）与点B重合，这时CDOE不是四边形，故x0=﹣6（舍去）．

∴E的坐标是（﹣2，﹣）．