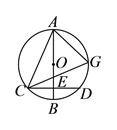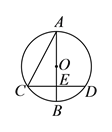Question

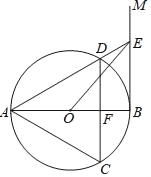
【题目】如图，AB是⊙O的直径，过点B作⊙O的切线BM，点A，C，D分别为⊙O的三等分点，连接AC，AD，DC，延长AD交BM于点E，CD交AB于点F．

（1）求证：CD∥BM；

（2）连接OE，若DE＝m，求△OBE的周长．

Answer 1

【答案】(1)见解析；（2）

【解析】

(1)由 点A、C、D为⊙O的三等分点，可证得△ACD为等边三角形，AB⊥CD ，BE⊥AB ，可得CD∥BM.

(2) 接DB，如图, 可得∠C＝60°，∠ABD＝∠C＝60°，∠DBE＝30°，

在Rt△DBE中，BE＝2DE＝2m，DB＝DE＝m．

在Rt△ADB中，AB＝2BD＝2m，则OB＝m，

在Rt△OBE中，OE＝＝m，

可得△OBE周长.

（1）证明：∵点A、C、D为⊙O的三等分点，

∴，

∴AD＝DC＝AC．

∴△ACD为等边三角形，

而点O为△ACD的外心，

∴AB⊥CD．

∵BM为⊙O的切线，

∴BE⊥AB．

∴CD∥BM；

（2）解：连接DB，如图，

∵△ACD为等边三角形，

∴∠C＝60°，

∴∠ABD＝∠C＝60°，

∴∠DBE＝30°，

在Rt△DBE中，BE＝2DE＝2m，DB＝DE＝m．

在Rt△ADB中，AB＝2BD＝2m，则OB＝m，

在Rt△OBE中，OE＝＝m，

∴△OBE周长为2m+m+m＝（2++）m．