题目内容
(12分)如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/s;同时直线PQ由点B出发,沿BA
的方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交
BC于点Q、交BD于点F.连接PM,设运动时间为ts(0<t<5).
(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为ycm2,求y与t之间的函数关系式;
(3)是否存在某一时刻t,使
 ?若存在,求出t的值;若不存在,说明理由;
?若存在,求出t的值;若不存在,说明理由;(4)连接PC,是否存在某一时刻t,使点M在线段PC的垂直平分线上?若存在,求出此时t的值;若不存在,说明理由.

解:(1)假设四边形PQCM是平行四边形,则PM∥QC,∴AP=AM
∴ ,解得
,解得
答:当 s时,四边形PQCM是平行四边形。
s时,四边形PQCM是平行四边形。
(2)过P作PE⊥AC,交AC于E。

∵PQ∥AC
∴△PBQ∽△ABC,∴△PBQ是等腰三角形,PQ=PB= ,
,
∴ ,即
,即 ,解得
,解得 ,
,
∴
又∵ ,
,
∴
答:y与t之间的函数关系式是
(3)
当 时,
时,


解得 ,
, (舍去)
(舍去)
答:当 时,S四边形PQCM=S△ABC
时,S四边形PQCM=S△ABC
(4)假设存在某一时刻t,使点M在线段PC的垂直平分线上,则MP=MC,
过M作MH⊥AB,交AB于H,由△AHM∽△ADB

∴ ,又
,又
∴ ,
,
∴
即
在Rt△HMP中,

又∵
由
∴
解得: (舍去)
(舍去)
答:当 s时,点M在线段PC的垂直平分线上。解析:
s时,点M在线段PC的垂直平分线上。解析:
略
∴
 ,解得
,解得
答:当
 s时,四边形PQCM是平行四边形。
s时,四边形PQCM是平行四边形。(2)过P作PE⊥AC,交AC于E。

∵PQ∥AC
∴△PBQ∽△ABC,∴△PBQ是等腰三角形,PQ=PB=
 ,
,∴
 ,即
,即 ,解得
,解得 ,
,∴

又∵
 ,
,∴

答:y与t之间的函数关系式是

(3)

当
 时,
时,

解得
 ,
, (舍去)
(舍去)答:当
 时,S四边形PQCM=S△ABC
时,S四边形PQCM=S△ABC(4)假设存在某一时刻t,使点M在线段PC的垂直平分线上,则MP=MC,
过M作MH⊥AB,交AB于H,由△AHM∽△ADB

∴
 ,又
,又
∴
 ,
,∴

即

在Rt△HMP中,

又∵

由

∴

解得:
 (舍去)
(舍去)答:当
 s时,点M在线段PC的垂直平分线上。解析:
s时,点M在线段PC的垂直平分线上。解析:略

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目


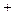 BD=AC,求∠B︰∠C 的比值
BD=AC,求∠B︰∠C 的比值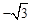 ),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).
),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).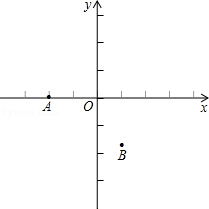
 cm/s的速度运动,连接BQ、PQ,设△BQP面积为S(cm2),点P、Q运动的时间为t(s),求S与t的函数关系式,并写出t的取值范围;
cm/s的速度运动,连接BQ、PQ,设△BQP面积为S(cm2),点P、Q运动的时间为t(s),求S与t的函数关系式,并写出t的取值范围;
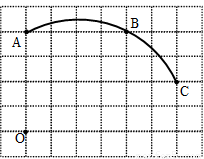
 )
)