题目内容
(2013年四川泸州12分)如图,在直角坐标系中,点A的坐标为(﹣2,0),点B的坐标为(1,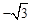 ),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).
),已知抛物线y=ax2+bx+c(a≠0)经过三点A、B、O(O为原点).
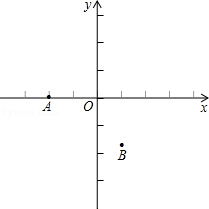
(1)求抛物线的解析式;
(2)在该抛物线的对称轴上,是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由;
(3)如果点P是该抛物线上x轴上方的一个动点,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.(注意:本题中的结果均保留根号)
解:(1)将A(﹣2,0),B(1, ),O(0,0)三点的坐标代入y=ax2+bx+c(a≠0),得:
),O(0,0)三点的坐标代入y=ax2+bx+c(a≠0),得:
 ,解得:
,解得: 。
。
∴所求抛物线解析式为 。
。
(2)存在。理由如下:
如答图①所示,

∵ ,
,
∴抛物线的对称轴为x=﹣1。
∵点C在对称轴x=﹣1上,△BOC的周长=OB+BC+CO。
∵OB=2,∴要使△BOC的周长最小,必须BC+CO最小。
∵点O与点A关于直线x=﹣1对称,有CO=CA,
△BOC的周长=OB+BC+CO=OB+BC+CA,
∴当A、C、B三点共线,即点C为直线AB与抛物线对称轴的交点时,BC+CA最小,此时△BOC的周长最小。
设直线AB的解析式为y=kx+t,则有:
 ,解得:
,解得: 。
。
∴直线AB的解析式为 。
。
当x=﹣1时, ,∴所求点C的坐标为(﹣1,
,∴所求点C的坐标为(﹣1, )。
)。
(3)设P(x,y)(﹣2<x<0,y<0),
则 ①
①
如答图②所示,过点P作PQ⊥y轴于点Q,PG⊥x轴于点G,过点A作AF⊥PQ轴于点F,过点B作BE⊥PQ轴于点E,则PQ=﹣x,PG=y,由题意可得:

 将①代入②得:
将①代入②得:
 ,
,
∴当x= 时,△PAB的面积最大,最大值为
时,△PAB的面积最大,最大值为 。
。
此时 。
。
∴点P的坐标为( ,
, )。
)。
【解析】(1)直接将A、O、B三点坐标代入抛物线解析式的一般式,可求解析式。
(2)因为点A,O关于对称轴对称,连接AB交对称轴于C点,C点即为所求,求直线AB的解析式,再根据C点的横坐标值,求纵坐标。
(3)设P(x,y)(﹣2<x<0,y<0),用割补法可表示△PAB的面积,根据面积表达式再求取最大值时,x的值。
考点:二次函数综合题,曲线上点的坐标与方程的关系,轴对称的应用(线段和最小的问题),由实际问题列函数关系式,二次函数最值,转换思想的应用。

 名校课堂系列答案
名校课堂系列答案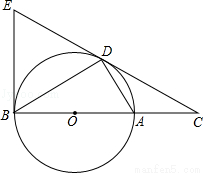
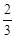 ,求BE的长.
,求BE的长.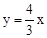 与反比例函数
与反比例函数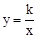 (x>0)的图象交于点A.将
(x>0)的图象交于点A.将
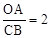 ,求反比例函数的解析式.
,求反比例函数的解析式.