题目内容
9.两条平行线被第三条直线所截,一组同位角的平分线的位置关系是互相平行(填“平行”或“垂直”).分析 此题利用平行线的性质:两直线平行,同位角相等.那么同位角的平分线所分得的角也相等,再根据同位角相等,两直线平行的判定就可证明.
解答 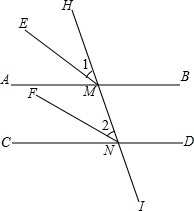 解:如图,AB∥CD,HI与AB,CD分别交于点M、N,EM,FN分别是∠AMH,∠CNH的平分线,
解:如图,AB∥CD,HI与AB,CD分别交于点M、N,EM,FN分别是∠AMH,∠CNH的平分线,
∵AB∥CD,
∴∠AMH=∠CNH(两直线平行,同位角相等),
∵EM,FN分别是∠AMH,∠CNH的平分线,
∴∠1=∠2,
∴EM∥FN(同位角相等,两直线平行),
∴∠1=$\frac{1}{2}$∠AMH,∠2=$\frac{1}{2}$∠CNH,
∴∠1=∠2,
∴EM∥FN(同位角相等,两直线平行).
故答案为:平行.
点评 本题主要考查了平行线的性质和判定,及角平分线的定义,综合利用平行线的性质及判定是解答此题的关键.

练习册系列答案
相关题目
2.计算$\sqrt{8}$×$\sqrt{\frac{1}{2}}$+($\sqrt{5}$)0的结果为( )
| A. | 2+$\sqrt{2}$ | B. | $\sqrt{2}$+1 | C. | 3 | D. | 5 |
1. 如图,用火柴棍摆出一系列三角形图案,按这种方法摆下去,第五个图案需要火柴棍总数为( )
如图,用火柴棍摆出一系列三角形图案,按这种方法摆下去,第五个图案需要火柴棍总数为( )
 如图,用火柴棍摆出一系列三角形图案,按这种方法摆下去,第五个图案需要火柴棍总数为( )
如图,用火柴棍摆出一系列三角形图案,按这种方法摆下去,第五个图案需要火柴棍总数为( )| A. | 31根 | B. | 42根 | C. | 45根 | D. | 51根 |
18.下列运算正确的是( )
| A. | 2-1=-2 | B. | m6÷m2=m4 | C. | $\sqrt{9}$=±3 | D. | (mn3)3=mn5 |
17.下列调查方式合适的是( )
| A. | 为了了解市民对电影《南京》的感受,小华在某校随机采访了8名初三学生 | |
| B. | 为了了解全校学生用于做数学作业的时间,小民同学在网上向3位好友做了调查 | |
| C. | 为了了解全国青少年儿童的睡眠时间,统计人员采用了普查的方式 | |
| D. | 为了了解“嫦娥一号”卫星零部件的状况,检测人员采用了普查的方式 |