题目内容

函数y=x2+mx-2（m＜0）的图象是（　　）
A、
B、
C、
D、
考点：二次函数的图象
专题：
分析：利用二次函数的性质a，b异号，则函数对称轴一定在y轴右侧，再利用a，c的值决定开口方向以及图象与y轴交点，进而得出答案．
解答：解：∵函数y=x2+mx-2（m＜0），
∴函数图象开口向上，函数对称轴一定在y轴右侧，且图象与y轴交于点（0，-2），
故符合题意的图象只有C．
故选：C．
点评：此题主要考查了函数图象的性质，正确把握a，b，c与图象的关系是解题关键．
练习册系列答案
相关题目
尺规作图：（不写作法，保留作图痕迹）已知线段a、b和∠α．
（1）作三角形△ABC，使∠B=∠α、AB=a、BC=b．
（2）作△ABC的高线CD．
如图，已知圆锥侧面展开图的扇形面积为65π cm2，扇形的弧长为10π cm，则圆锥的高是（　　）
A、5cmB、10cm
C、12cmD、13cm
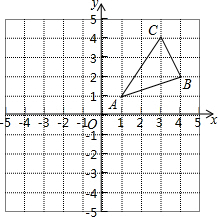如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．
（1）请画出△ABC向左平移5个单位长度后得到的△A1B1C1；
（2）把△ABC绕A点顺时针旋转90°得到△AB2C2，请画出△AB2C2，并写出B2的坐标．
若关于x的一元二次方程kx2-2x-1=0有两个实数根，则k的取值范围是
 
．
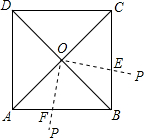如图，正方形纸片ABCD对角线AC，BD交于点O，将一根木条的一端固定在点O处，此时木条与BC交于点E，将木条绕点O顺时针旋转90°，此时木条与AB交于点F
（1）请问OE与OF相等吗？并证明你的猜想；
（2）若木条OP=4cm，求木条OP旋转中所扫过的面积．
有理数a，b在数轴上的位置如图所示，则下列判断正确的是（　　）
A、ab＞0
B、
a
b
＞0
C、a＜b
D、a＞0＞b
估算3
7
在连续整数
 
和
 
之间．
一条弧所对的圆心角为60°，那么这条弧所对的圆周角为（　　）
A、30°B、60°
C、120°D、150°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网