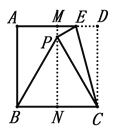��Ŀ����
����Ŀ����ͼ1����֪����ABED����C�DZ�DE���е㣬��AB=2AD.
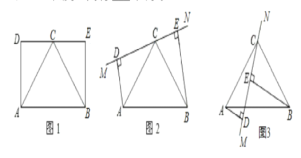
(1)��ͼ1ͨ���۲졢������Եõ��߶�AC���߶�BC��������ϵΪ___��λ�ù�ϵΪ__��
(2)����ͼ1�еġ�ABC�̶�����,�Ƶ�C��תDE���ڵ�ֱ��MN��ͼ2�е�λ��(������AD��BE��ֱ��MN��ͬ��).��̽���߶�AD��BE��DE����֮����ʲô��ϵ?������֤��(��һ���еõ��IJ�����ۿ���ֱ����֤����ʹ��)��
(3)����ͼ2�еġ�ABC�̶�����,�����Ƶ�C��תDE���ڵ�ֱ��MN��ͼ3�е�λ��(�����߶�AD��BE��ֱ��MN�����).��̽���߶�AD��BE��DE����֮����___��ϵ.
���𰸡���1��AC=BC��AC��BC������2��DE=AD+BE�����ɼ���������3��DE=BEAD.
��������
��1�����ݾ��ε����ʼ����ɶ���������֤����ADC�ա�BEC������ȫ�������ε����ʼ��ɵõ����ۣ�
��2��ͨ��֤����ACD�ա�CBE������ȫ�������ε����ʵó����ɵ��߶�AD��BE��DE����֮��Ĺ�ϵ��
��3��ͨ��֤����ACD�ա�CBE������ȫ�������ε����ʵó����ɵ��߶�AD��BE��DE����֮��Ĺ�ϵ��
(1)AC=BC��AC��BC��
����ADC����BEC��, ��
��
���ADC�ա�BEC(SAS)��
��AC=BC����DCA=��ECB.
��AB=2AD=DE��DC=CE��
��AD=DC��
���DCA=45����
���ECB=45����
���ACB=180����DCA��ECB=90��.
��AC��BC��
�ʴ�Ϊ��AC=BC��AC��BC��
(2)DE=AD+BE.�������£�
�ߡ�ACD=��CBE=90����BCE��
����ACD����CBE��, ��
��
���ACD�ա�CBE(AAS)��
��AD=CE��DC=EB.
��DC+CE=BE+AD��
��DE=AD+BE.
(3)DE=BEAD.�������£�
�ߡ�ACD=��CBE=90����BCE��
����ACD����CBE��,
 ��
��
���ACD�ա�CBE(AAS)��
��AD=CE��DC=EB.
��DCCE=BEAD��
��DE=BEAD��
�ʴ�Ϊ��DE=BEAD.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�