题目内容
边长为2的正六边形的边心距为 ___ __ ．
．
【解析】
试题分析：连接OA、OB、OC、OD、OE、OF，∵正六边形ABCDEF，∴∠AOB=∠BOC=∠COD=∠DOE=∠EOF=∠AOF，∴∠AOB=360°÷6=60°，OA=OB，∴△AOB是等边三角形，∴OA=OB=AB=2，∵OM⊥AB，∴AM=BM=1，在△OAM中，由勾股定理得：OM=
=．故答案为：．
考点：正多边形和圆．
练习册系列答案
阅读快车系列答案
相关题目
在Rt△ABC中， ∠C=Rt∠ ,AC=3cm， AB=5cm,若以C为圆心，4cm为半径画一个圆，则下列结论中，正确的是（ ）
| A．点A在圆C内，点B在圆C外 |
| B．点A在圆C外，点B在圆C内 |
| C．点A在圆C上，点B在圆C外 |
| D．点A在圆C内，点B在圆C上 |
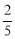，那么n等于（ ）
（
）的图象如下图所示，且关于x的一元二次方程
没有实数根，有下列结论：①
；②
；③
．其中，正确结论的个数是（ ）
