题目内容
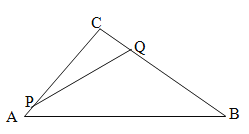
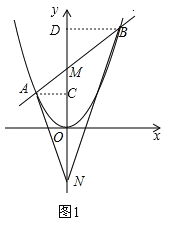
【题目】如图1,直线y=x+1与抛物线![]() 相交于A、B两点,与y轴交于点M,M、N关于x轴对称,连接AN、BN.
相交于A、B两点,与y轴交于点M,M、N关于x轴对称,连接AN、BN.
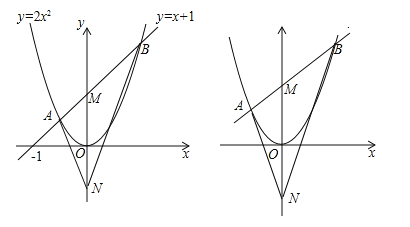
(1)①求A、B的坐标;②求证:∠ANM=∠BNM;
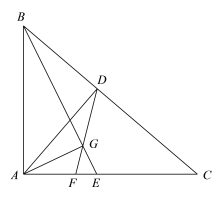
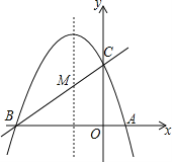
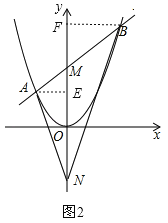
(2)如图2,将题中直线y=x+1变为y=kx+b(b>0),抛物线![]() 变为
变为![]() (a>0),其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.
(a>0),其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.
【答案】(1)①A(![]() ,
,![]() ),B( 1,2);②证明见解析;(2)成立,理由见解析.
),B( 1,2);②证明见解析;(2)成立,理由见解析.
【解析】
(1)①联立直线和抛物线解析式可求得A、B两点的坐标;②过A作AC⊥y轴于C,过B作BD⊥y轴于D,可分别求得∠ANM和∠BNM的正切值,可证得结论;
(2)当k=0时,由对称性可得出结论;当k≠0时,过A作AE⊥y轴于E,过B作BF⊥y轴于F,设A(![]() ,
,![]() )、B(
)、B(![]() ,
,![]() ),联立直线和抛物线解析式,消去y,利用根与系数的关系,可求得
),联立直线和抛物线解析式,消去y,利用根与系数的关系,可求得![]() ,则可证明Rt△AEN∽Rt△BFN,可得出结论.
,则可证明Rt△AEN∽Rt△BFN,可得出结论.
解:(1)①由已知得![]() ,解得
,解得![]() 或x=1,当
或x=1,当![]() 时,y=
时,y=![]() ,当x=1时,y=2,∴A、B两点的坐标分别为(
,当x=1时,y=2,∴A、B两点的坐标分别为(![]() ,
,![]() ),( 1,2);
),( 1,2);
②如图1,过A作AC⊥y轴于C,过B作BD⊥y轴于D,由①及已知有A(![]() ,
,![]() ),B( 1,2),且OM=ON=1,∴tan∠ANM=
),B( 1,2),且OM=ON=1,∴tan∠ANM=![]() =
=![]() =
=![]() ,tan∠BNM=
,tan∠BNM=![]() =
=![]() =
=![]() ,∴tan∠ANM=tan∠BNM,∴∠ANM=∠BNM;
,∴tan∠ANM=tan∠BNM,∴∠ANM=∠BNM;
(2)∠ANM=∠BNM成立,①当k=0,△ABN是关于y轴的轴对称图形,∴∠ANM=∠BNM;
②当k≠0,根据题意得:OM=ON=b,设A(![]() ,
,![]() )、B(
)、B(![]() ,
,![]() ).
).
如图2,过A作AE⊥y轴于E,过B作BF⊥y轴于F,由题意可知:ax2=kx+b,即ax2﹣kx﹣b=0,∴![]() ,
,![]() ,∵
,∵![]()
![]()
=![]() =
=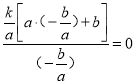 ,
,
∴![]() ,
,
∴Rt△AEN∽Rt△BFN,
∴∠ANM=∠BNM.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目