题目内容
把下列各式分解因式:
(1)a5-a;
(2)-3x3-12x2+36x;
(3)9-x2+12xy-36y2;
(4)a2+2ab+b2-a-b;
(5)(m2+3m)2-8(m2+3m)-20;
(6)4a2bc-3a2c2+8abc-6ac2;
(7)(y2+3y)-(2y+6)2.
(1)a5-a;
(2)-3x3-12x2+36x;
(3)9-x2+12xy-36y2;
(4)a2+2ab+b2-a-b;
(5)(m2+3m)2-8(m2+3m)-20;
(6)4a2bc-3a2c2+8abc-6ac2;
(7)(y2+3y)-(2y+6)2.
考点:提公因式法与公式法的综合运用,因式分解-分组分解法
专题:
分析:(1)首先提取公因式a,进而利用平方差公式分解因式得出即可;
(2)首先提取公因式-3x,进而利用十字相乘法分解因式得出;
(3)首先将后三项分组,利用完全平方公式分解因式,进而利用平方差公式分解即可;
(4)首先将前三项分组,利用完全平方公式分解因式,进而利用提取公因式法分解即可;
(5)利用十字相乘法分解因式得出即可;
(6)直接利用提取公因式法分解因式进而得出即可;
(7)首先利用平方差公式分解因式,进而利用十字相乘法分解因式得出.
(2)首先提取公因式-3x,进而利用十字相乘法分解因式得出;
(3)首先将后三项分组,利用完全平方公式分解因式,进而利用平方差公式分解即可;
(4)首先将前三项分组,利用完全平方公式分解因式,进而利用提取公因式法分解即可;
(5)利用十字相乘法分解因式得出即可;
(6)直接利用提取公因式法分解因式进而得出即可;
(7)首先利用平方差公式分解因式,进而利用十字相乘法分解因式得出.
解答:解:(1)a5-a
=a(a4-1)
=a(a2+1)(a2-1)
=a(a2+1)(a+1)(a-1);
(2)-3x3-12x2+36x
=-3x(x2+4x-12)
=-3x(x+6)(x-2);
(3)9-x2+12xy-36y2
=9-(x2-12xy+36y2)
=9-(x-6y)2
=(3+x-6y)(3-x+6y);
(4)a2+2ab+b2-a-b
=(a+b)2-(a+b)
=(a+b)(a+b-1);
(5)(m2+3m)2-8(m2+3m)-20
=(m2+3m-10)(m2+3m+2)
=(m+5)(m-2)(m+2)(m+1);
(6)4a2bc-3a2c2+8abc-6ac2
=ac(4ab-3ac+8b-6c)
=ac[a(4b-3c)+2(4b-3c)]
=ac(4b-3c)(a+2);
(7)(y2+3y)-(2y+6)2
=(y2+3y+2y+6)(y2+3y-2y-6)
=(y2+5y+6)(y2+y-6)
=(y+2)(y+30(y-2)(y+3).
=a(a4-1)
=a(a2+1)(a2-1)
=a(a2+1)(a+1)(a-1);
(2)-3x3-12x2+36x
=-3x(x2+4x-12)
=-3x(x+6)(x-2);
(3)9-x2+12xy-36y2
=9-(x2-12xy+36y2)
=9-(x-6y)2
=(3+x-6y)(3-x+6y);
(4)a2+2ab+b2-a-b
=(a+b)2-(a+b)
=(a+b)(a+b-1);
(5)(m2+3m)2-8(m2+3m)-20
=(m2+3m-10)(m2+3m+2)
=(m+5)(m-2)(m+2)(m+1);
(6)4a2bc-3a2c2+8abc-6ac2
=ac(4ab-3ac+8b-6c)
=ac[a(4b-3c)+2(4b-3c)]
=ac(4b-3c)(a+2);
(7)(y2+3y)-(2y+6)2
=(y2+3y+2y+6)(y2+3y-2y-6)
=(y2+5y+6)(y2+y-6)
=(y+2)(y+30(y-2)(y+3).
点评:此题主要考查了提取公因式法分解因式以及分组分解法分解因式,熟练应用乘法公式是解题关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
若二次函数y=ax2的图象经过点P(2,8),则该图象必经过点( )
| A、(2,-8) |
| B、(-2,8) |
| C、(8,-2) |
| D、(-8,2) |
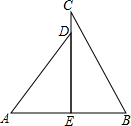 两个直角三角形按如图方式摆放,若AD=10,BE=6,∠ADE=37°,∠BCE=29°.求CD长(精确到0.01).
两个直角三角形按如图方式摆放,若AD=10,BE=6,∠ADE=37°,∠BCE=29°.求CD长(精确到0.01). 如图,菱形ABCD的边长是2cm,E是AB中点,且DE⊥AB,则DE的长为
如图,菱形ABCD的边长是2cm,E是AB中点,且DE⊥AB,则DE的长为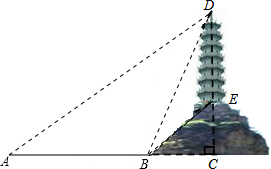 兴趣小组在一次数学实践活动中,为了测量如图所示的小山顶的塔高,进行了如下的操作,首先在A处测得塔尖D的仰角为30°,然后沿AC方向前进72米到达山脚B处,此时测得塔尖D的仰角为60°,塔底E的仰角为45°,求塔高.(结果保留根号)
兴趣小组在一次数学实践活动中,为了测量如图所示的小山顶的塔高,进行了如下的操作,首先在A处测得塔尖D的仰角为30°,然后沿AC方向前进72米到达山脚B处,此时测得塔尖D的仰角为60°,塔底E的仰角为45°,求塔高.(结果保留根号)