Question

5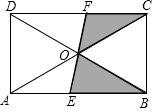．如图，EF过矩形的对角线的交点O，且分别交AB、CD于点E、F，如果阴影部分面积为12，那么矩形的面积为（　　）

• A． 60
• B． 30
• C． 40
• D． 48

Answer 1

分析 根据矩形的性质得到OA=OC，AB∥DC，推出∠DCA=∠CAB，∠CFE=∠AEF，证△CFO≌△AEO，求出△CFO的面积等于△AEO的面积，求出△OAB的面积即可．

解答 解：∵矩形ABCD，
∴OA=OC，AB∥DC，
∴∠DCA=∠CAB，∠CFE=∠AEF，
∴△CFO≌△AEO，
∴△CFO的面积等于△AEO的面积，
∵图中阴影部分的面积为12，
∴△AOB的面积是6，
∵矩形ABCD，OB=OD，
∴矩形ABCD的面积是4×12=48．
故选D．

点评 本题主要考查对矩形的性质，全等三角形的性质和判定，三角形的面积，平行线的性质等知识点的理解和掌握，能求出△AOB的面积是解此题的关键