题目内容
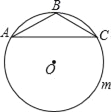
【题目】如图,△ABC中,AB=BC,∠ABC=120°,AC=2![]() ,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
,⊙O是△ABC的外接圆,D是优弧AmC上任意一点(不包括A,C),记四边形ABCD的周长为y,BD的长为x,则y关于x的函数关系式是( )
A. y=![]() x+4 B. y=
x+4 B. y=![]() x+4 C. y=
x+4 C. y=![]() x2+4 D. y=
x2+4 D. y=![]() x2+4
x2+4
【答案】B
【解析】分析:作辅助线,构建全等三角形和等边三角形,证明Rt△AGB≌Rt△CFB得:AG=CF,根据30°角的笥质表示DF和DG的长,计算四边形ABCD的周长即可.
详解:连接OB交AC于E,连接OC、OB,
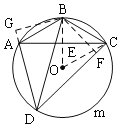
过B作BG⊥AD,BF⊥CD,交DA的延长线于G,交CD于F,
∵AB=BC,
∴![]() ,
,
∴∠BDA=∠BDC,
∴BG=BF,
在Rt△AGB和Rt△CFB中,
∵![]() ,
,
∴Rt△AGB≌Rt△CFB,
∴AG=FC,
∵![]() ,
,
∴OB⊥AC,EC=![]() AC=
AC=![]() ×2
×2![]() =
=![]() ,
,
在△AOB和△COB中,
∵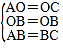 ,
,
∴△AOB≌△COB(SSS),
∴∠ABO=∠OBC=![]() ∠ABC=
∠ABC=![]() ×120°=60°,
×120°=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴∠BOC=60°,
∴∠BDC=∠ADB=30°,
Rt△BDF中,BD=x,
∴DF=![]() x,
x,
同理得:DG=![]() x,
x,
∴AD+DC=AD+DF+FC=DG+DF=![]() x+
x+![]() x=
x=![]() x,
x,
Rt△BEC中,∠BCA=30°,
∴BE=1,BC=2,
∴AB=BC=2,
∴y=AB+BC+AD+DC=2+2+![]() x=
x=![]() x+4,
x+4,
故选B.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目