题目内容
15．
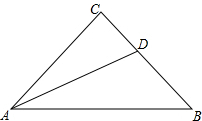如图，已知AD为等腰三角形ABC的底角的平分线，∠C=90°，求证：AB=AC+CD．
分析 作DE⊥AB于E，根据等腰三角形的性质证明DE=BE，根据角平分线的性质得到CD=DE，证明△CAD≌△EAD，得到AC=AE，得到答案．
解答 证明：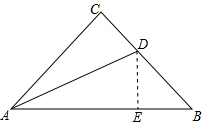
作DE⊥AB于E，
∵△ABC是等腰直角三角形，
∴∠B=45°，又DE⊥AB，
∴DE=BE，
∵AD为△ABC的底角的平分线，∠C=90°，DE⊥AB，
∴DE=DC，
则CD=BE，
在△CAD和△EAD中，
$\left\{\begin{array}{l}{∠C=∠AED}\\{∠CAD=∠EAD}\\{AD=AD}\end{array}\right.$，
∴△CAD≌△EAD，
∴AC=AE，
AB=AE+EB=AC+CD．
点评 本题考查的是角平分线的性质、全等三角形的判定和性质，掌握角的平分线上的点到角的两边的距离相等是解题的关键．
练习册系列答案
相关题目
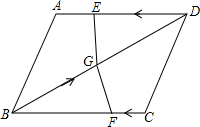如图，在四边形ABCD中，AD=BC=10，AB=CD，BD=12，点E从D点出发，以每秒1个单位的速度沿DA向点A匀速移动，点F从点C出发，以每秒3个单位的速度沿C→B→C，作匀速移动，点G从点B出发沿BD向点D匀速移动，三个点同时出发，当有一个点到达终点时，其余两点也随之停止运动，假设移动时间为t秒．
3．下列代数式中a，-2ab，x+y，x2+y2，-1，单项式共有（ ）
| A． | 3个 | B． | 4个 | C． | 5个 | D． | 6个 |
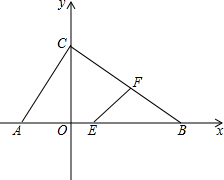如图，在平面直角坐标系中，△ABC的顶点都在坐标轴上，OA=2，OC=3，OB=4．点E，F分别是线段AB，BC上的动点（不与端点A，B重合），点E从点A出发沿x轴正方向以每秒2个单位长度的速度向点B运动，同时点F从点B出发沿线段BC方向以每秒1个单位长度的速度向点C运动（当点E停止时，点F也同时停止），当两个动点运动了t秒时，解答下列问题：
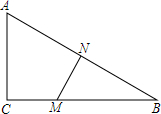已知△ABC，∠ACB=90°，AC=4，MN垂直平分AB，且BM=2CM，求CM的长．
7．如果A是x的二次多项式，B是x的四次多项式，那么A-B是（ ）
| A． | 三次多项式 | B． | 二次多项式 | C． | 四次多项式 | D． | 五次多项式 |