题目内容
已知:∠C=Rt∠,∠A、∠B、∠C的对边为a、b、c,且a:b=3:4,a+b=c+4.
(1)求a、b、c 的值;
(2)已知AB上有一点E,并以BE为直径画圆,并且这个圆与AC相切于D点,求该圆的半径.
(1)求a、b、c 的值;
(2)已知AB上有一点E,并以BE为直径画圆,并且这个圆与AC相切于D点,求该圆的半径.
考点:圆的综合题
专题:
分析:(1)根据a:b=3:4,设a=3k,b=4k.根据勾股定理,得c=5k;再根据a+b=c+4,求得k的值,从而求得a,b,c的长;
(2)根据题意画出图形,设该圆的半径为r,连接OD,由切线的性质可知OD⊥AC,故可得出OD∥BC,所以△AOD∽△ABC,再根据相似三角形的对应边成比例即可得出r的值.
(2)根据题意画出图形,设该圆的半径为r,连接OD,由切线的性质可知OD⊥AC,故可得出OD∥BC,所以△AOD∽△ABC,再根据相似三角形的对应边成比例即可得出r的值.
解答: 解:(1)∵a:b=3:4,
解:(1)∵a:b=3:4,
∴设a=3k,则b=4k.
∴c=
=
=5k,
又∵a+b=c+4,
∴3k+4k=5k+4,解得k=2.
∴a=6,b=8,c=10;
(2)如图所示:设该圆的半径为r,连接OD,
∵点D是AC与⊙O的切点,
∴OD⊥AC,
∵BC⊥AC,
∴OD∥BC,
∴△AOD∽△ABC,
∴
=
,
=
,解得r=
.
 解:(1)∵a:b=3:4,
解:(1)∵a:b=3:4,∴设a=3k,则b=4k.
∴c=
| a2+b2 |
| (3k)2+(4k)2 |
又∵a+b=c+4,
∴3k+4k=5k+4,解得k=2.
∴a=6,b=8,c=10;
(2)如图所示:设该圆的半径为r,连接OD,
∵点D是AC与⊙O的切点,
∴OD⊥AC,
∵BC⊥AC,
∴OD∥BC,
∴△AOD∽△ABC,
∴
| OA |
| AB |
| OD |
| BC |
| 10-r |
| 10 |
| r |
| 6 |
| 15 |
| 4 |
点评:本题考查的是圆的综合题,根据题意画出图形,利用相似三角形的性质求解是解答此题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
不等式组
的解集在数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
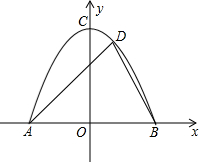 某公路隧道横截面为抛物线,其最大高度为8米,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,抛物线解析式为y=-
某公路隧道横截面为抛物线,其最大高度为8米,以隧道底部宽AB所在直线为x轴,以AB垂直平分线为y轴建立如图所示的平面直角坐标系,抛物线解析式为y=-
 如图,直角三角形纸片ABC中,∠ACB=90°,AC=4,BC=3.折叠纸片,使顶点A落在直角边BC上的点A′处,折痕MN分别交AC、AB于点M、N.若NA′⊥BC,则A′B的长为
如图,直角三角形纸片ABC中,∠ACB=90°,AC=4,BC=3.折叠纸片,使顶点A落在直角边BC上的点A′处,折痕MN分别交AC、AB于点M、N.若NA′⊥BC,则A′B的长为 如图,△ABC≌△DEF,且这两个三角形都是三边互不相等的锐角三角形.现用这两个
如图,△ABC≌△DEF,且这两个三角形都是三边互不相等的锐角三角形.现用这两个