题目内容
已知抛物线y=-x2+ax+
,直线y=2x
(1)求证:抛物线与直线相交;
(2)求档抛物线的顶点在直线的下方时,a的取值范围;
(3)当a在(2)的取值范围内时,求抛物线截直线所得弦长的最小值.
| 1 |
| 2 |
(1)求证:抛物线与直线相交;
(2)求档抛物线的顶点在直线的下方时,a的取值范围;
(3)当a在(2)的取值范围内时,求抛物线截直线所得弦长的最小值.
考点:二次函数综合题
专题:压轴题
分析:(1)联立两函数解析式消掉y得到关于x的一元二次方程,再利用根的判别式证明;
(2)把函数解析式整理成顶点式解析式,然后根据抛物线顶点在直线下方列出不等式,然后求解即可;
(3)求出两交点的横坐标的差值,然后解直角三角形表示出弦长,再利用二次函数的最值问题解答即可.
(2)把函数解析式整理成顶点式解析式,然后根据抛物线顶点在直线下方列出不等式,然后求解即可;
(3)求出两交点的横坐标的差值,然后解直角三角形表示出弦长,再利用二次函数的最值问题解答即可.
解答:解:(1)由题意得,-x2+ax+
=2x,
整理得,x2+(2-a)x-
=0,
△=b2-4ac=(2-a)2-4×1×(-
)=(2-a)2+2≥2,
所以,方程有两个不相等的实数根,
所以,抛物线与直线相交;
(2)∵y=-x2+ax+
=-(x-
)2+
+
,
∴抛物线的顶点坐标为(
,
+
),
∵抛物线的顶点在直线的下方,
∴
+
<2×
,
∴a2-4a+2<0,
解得2-
<a<2+
;
(3)设x2-(2-a)x-
=0的两个根分别为x1,x2,
则x1+x2=a-2,x1•x2=-
,
|x1-x2|=
=
,
∵两交点在直线y=2x上,
∴弦长=
|x1-x2|=
,
∵2-
<a<2+
,
∴当a=2时,弦长有最小值
×
=
.
| 1 |
| 2 |
整理得,x2+(2-a)x-
| 1 |
| 2 |
△=b2-4ac=(2-a)2-4×1×(-
| 1 |
| 2 |
所以,方程有两个不相等的实数根,
所以,抛物线与直线相交;
(2)∵y=-x2+ax+
| 1 |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
| 1 |
| 2 |
∴抛物线的顶点坐标为(
| a |
| 2 |
| a2 |
| 4 |
| 1 |
| 2 |
∵抛物线的顶点在直线的下方,
∴
| a2 |
| 4 |
| 1 |
| 2 |
| a |
| 2 |
∴a2-4a+2<0,
解得2-
| 2 |
| 2 |
(3)设x2-(2-a)x-
| 1 |
| 2 |
则x1+x2=a-2,x1•x2=-
| 1 |
| 2 |
|x1-x2|=
(a-2)2-4×(-
|
| (a-2)2+2 |
∵两交点在直线y=2x上,
∴弦长=
| 5 |
| 5 |
| (a-2)2+2 |
∵2-
| 2 |
| 2 |
∴当a=2时,弦长有最小值
| 5 |
| 2 |
| 10 |
点评:本题是二次函数综合题型,主要利用了根的判别式,利用二次函数与不等式求不等式的关系,根与系数的关系,难点在于(3)根据直线解析式利用两交点的横坐标表示出弦长.

练习册系列答案
相关题目
 将两张宽度都为1的纸条叠放成如图所示的图形,所成四边形的锐角为α,则这个四边形的面积为( )
将两张宽度都为1的纸条叠放成如图所示的图形,所成四边形的锐角为α,则这个四边形的面积为( )A、
| ||
| B、tanα | ||
C、
| ||
D、
|
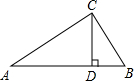 如图,∠ACB=90°,CD⊥AB于D.则:
如图,∠ACB=90°,CD⊥AB于D.则: 在圆O中,∠ACB=∠BCA=60°,AC=2
在圆O中,∠ACB=∠BCA=60°,AC=2 如图,在△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,若∠B=60°,∠C=70°,求∠EDF的度数.
如图,在△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,若∠B=60°,∠C=70°,求∠EDF的度数. 如图所示,回答各题的方位角:
如图所示,回答各题的方位角: 如图,∠1=∠2=115°,∠3=65°,图中有哪些直线互相平行.
如图,∠1=∠2=115°,∠3=65°,图中有哪些直线互相平行.