题目内容
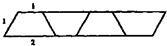
观察下图,解答后面的问题.
(1)把表中的空格填上适当的数据;
| 梯形个数 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 周长 | 5 | 8 | 11 | 14 | … |
(3)求n=2004时L的值;
(4)求L=6026时n的值.
解:(1)每一个数比前一个数多3,故填14+3=17,17+3=20;
(2)梯形周长=(上底+下底)+两腰长,n个梯形周长是L=n(上底+下底)+两腰长=n(1+2)+2=3n+2;
(3)当n=2004时,L=3×2004=6014;
(4)当L=6026时,3n+2=6026,解得n=2008.
分析:此题先根据图形的特点,找出周长L和梯形个数n之间的关系式L=n(1+2)+2=3n+2,然后根据关系式L=n(1+2)+2=3n+2解出(3)(4).
点评:本题是一道结论开放性题目,很好的体现了探究的过程:由具体数据得到一般规律,利用规律解决问题来验证规律的正确性.有利于培养同学们的探索发现意识.
(2)梯形周长=(上底+下底)+两腰长,n个梯形周长是L=n(上底+下底)+两腰长=n(1+2)+2=3n+2;
(3)当n=2004时,L=3×2004=6014;
(4)当L=6026时,3n+2=6026,解得n=2008.
分析:此题先根据图形的特点,找出周长L和梯形个数n之间的关系式L=n(1+2)+2=3n+2,然后根据关系式L=n(1+2)+2=3n+2解出(3)(4).
点评:本题是一道结论开放性题目,很好的体现了探究的过程:由具体数据得到一般规律,利用规律解决问题来验证规律的正确性.有利于培养同学们的探索发现意识.

练习册系列答案
相关题目