题目内容
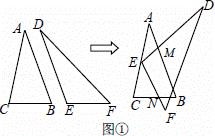
如图①,△ABC与△DEF是将△ACF沿过A点的某条直线剪开得到的(AB,DE是同一条剪切线).平移△DEF使顶点E与AC的中点重合,再绕点E旋转△DEF,使ED,E F分别与AB,BC交于M,N两点.
F分别与AB,BC交于M,N两点.
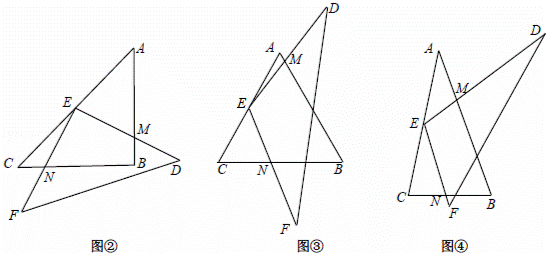
(1)如图②,△ABC中,若AB=BC,且∠ABC=90°,则线段EM与EN有何数量关系?请直接写出结论;
(2)如图③,△ABC中,若AB=BC,那么(1)中的结论是否还成立?若成立,请给出证明:若不成立,请说明理由;
(3)如图④,△ABC中,若AB:BC=m:n,探索线段EM与EN的数量关系,并证明你的结论.
解:(1)EM=EN.
证明:过点E作EG⊥BC,G为垂足,作EH⊥AB,H为垂足,连接BE,如答图②所示.
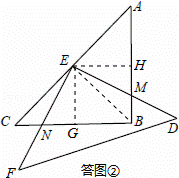
则∠EHB=∠EGB=90°.
∴在四边形BHEG中,∠HBG+∠HEG=180°.
∵∠HBG+∠DEF=180°,
∴∠HEG=∠DEF.
∴∠HEM=∠GEN.
∵BA=BC,点E为AC中点,
∴BE平分∠ABC.
又∵EH⊥AB,EG⊥BC,
∴EH=EG.
在△HEM和△GEN中,
∵∠ HEM=∠GEN,EH=EG,∠EHM=∠EGN,
HEM=∠GEN,EH=EG,∠EHM=∠EGN,
∴△HEM≌△GEN.
∴EM=EN.
(2)EM=EN仍然成立.
证明:过点E作EG⊥BC,G为垂足,作EH⊥AB,H为垂足,连接BE,如答图③所示.

则∠EHB=∠EGB=90°.
∴在四边形BHEG中,∠HBG+∠HEG=180°.
∵∠HBG+∠DEF=180°,
∴∠HEG=∠DEF.
∴∠HEM=∠GEN.
∵BA=BC,点E为AC中点,
∴BE平分∠ABC.
又∵EH⊥AB,EG⊥BC,
∴EH=EG.
在△HEM和△GEN中,
∵∠HEM=∠GEN,EH=EG,∠EHM=∠EGN,
∴△HEM≌△GEN.
∴EM=EN.
(3)线段EM与EN满足关系:EM:EN=n:m.
证明:过点E作EG⊥BC,G为垂足,作EH⊥AB,H为垂足,连接BE,如答图④所示.
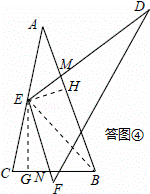
则∠EHB=∠EGB=90°.
∴在四边形BHEG中,∠HBG+∠HEG=180°.
∵∠HBG+∠DEF=180°,
∴∠HEG=∠DEF.
∴∠HEM=∠GEN.
∵∠HEM= ∠GEN,∠EHM=∠EGN,
∠GEN,∠EHM=∠EGN,
∴△HEM∽△GEN.
∴EM:EN=EH:EG.
∵点E为AC的中点,
∴S△AEB=S△CEB.
∴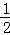 AB•EH=
AB•EH=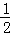 BC•EG.
BC•EG.
∴EH:EG=BC:AB.
∴EM:EN=BC:AB.
∵AB:BC=m:n,
∴EM:EN=n:m.

下列运算正确的是( )
|
| A. | a2+a3=a5 | B. | (﹣2a2)3=﹣6a6 | C. | (2a+1)(2a﹣1)=2a2﹣1 | D. | (2a3﹣a2)÷a2=2a﹣1 |
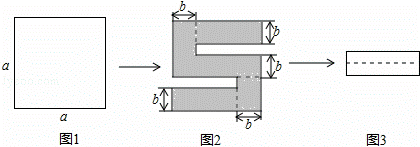
如图1,将一个边长为a的 正方形纸片剪去两个小矩形,得到一个“
正方形纸片剪去两个小矩形,得到一个“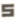 ”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
”的图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示,则新矩形的周长可表示为( )
|
| A. | 2a﹣3b | B. | 4a﹣8b | C. | 2a﹣4b | D. | 4a﹣10b |
已知a>b且a+b=0,则( )
|
| A. | a<0 | B. | b>0 | C. | b≤0 | D. | a>0 |
 是一个( )
是一个( ) .
.

 在双曲线y=﹣的两支上,若y1+y2>0,则x1+x2的范围是
在双曲线y=﹣的两支上,若y1+y2>0,则x1+x2的范围是