题目内容
1.小亮在某一时刻测得小树高为1.5m,其影长为1.2m,当他测量教学楼旁的一棵大树影长时,因大树靠近教学楼,它的一部分影子便落在了教学楼的墙上,经测量,地面部分影长为6.4m,墙上影长为2m,那么这棵大树高为多少米?分析 根据在同一时刻,不同物体的物高和影长成比例计算.
解答 解:设被挡部分的影长为xm,则
$\frac{1.5}{1.2}$=$\frac{2}{x}$,
解得:x=1.6,
设树高为ym,则
$\frac{1.5}{1.2}$=$\frac{y}{1.6+6.4}$,
解得:y=10,
答:树高为10m.
点评 本题考查了相似三角形的应用以及平行投影特点,注意在同一时刻,不同物体的物高和影长成比例.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.当x=-5,y=3时,代数式2x+3y的值是( )
| A. | -1 | B. | 1 | C. | -19 | D. | 19 |
16.端午节吃粽子是中华民族的传统习惯,妈妈买了4只红豆粽、2只碱水粽、5只干肉粽,粽子除内部馅料不同外其它均相同,小颖随意吃一个,吃到红豆粽的概率是( )
| A. | $\frac{1}{11}$ | B. | $\frac{1}{4}$ | C. | $\frac{4}{11}$ | D. | $\frac{1}{5}$ |
13.下列各式中正确的是( )
| A. | $\frac{1}{{\sqrt{2}-1}}=\sqrt{2}-1$ | B. | $\frac{1}{{\sqrt{50}}}=\frac{{\sqrt{2}}}{5}$ | C. | $\sqrt{1000}=10\sqrt{5}$ | D. | $\sqrt{9-2\sqrt{14}}=\sqrt{7}-\sqrt{2}$ |
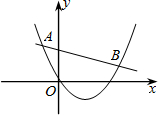 已知二次函数y1=ax2+bx+c与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2).如图所示,则能使y1>y2成立的x的取值范围是x<-2或x>8.
已知二次函数y1=ax2+bx+c与一次函数y2=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2).如图所示,则能使y1>y2成立的x的取值范围是x<-2或x>8.
 如图,△ABC的面积为32cm2,点D、E、F、G分别为AC,BD,BC,EC的中点,则△EFG的面积为2cm2.
如图,△ABC的面积为32cm2,点D、E、F、G分别为AC,BD,BC,EC的中点,则△EFG的面积为2cm2.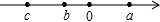 若有理数a,b,c在数轴上的位置如图所示,请化简:|ab3|=-ab3;|a+c|=-a-c;|b-c|=b-c;|b-c|-|b-a|=2b-c-a.
若有理数a,b,c在数轴上的位置如图所示,请化简:|ab3|=-ab3;|a+c|=-a-c;|b-c|=b-c;|b-c|-|b-a|=2b-c-a.