题目内容
3.观察下列各式:$\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$;$\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$;$\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$…请你将猜想到的规律用自然数n的代数式表示出来:$\sqrt{n+\frac{1}{n+2}}=(n+1)\sqrt{\frac{1}{n+2}}$,.分析 认真观察,可发现根号内第一个数和第二个数的分母相差为2,结果为第一个数和第二个数的分母和的一半与第二个数的算术平方根的积.
解答 解:根据式子可得:根号内第一个数和第二个数的分母相差为2,结果为第一个数和第二个数的分母和的一半与第二个数的算术平方根的积;
所以规律用自然数n的代数式表示为:$\sqrt{n+\frac{1}{n+2}}=(n+1)\sqrt{\frac{1}{n+2}}$,
故答案为:$\sqrt{n+\frac{1}{n+2}}=(n+1)\sqrt{\frac{1}{n+2}}$,
点评 解答此类题目的关键是认真观察题中式子的特点,找出其中的规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 如图,矩形ABCD的对角线AC=20,BC=16,则图中五个小矩形的周长之和为( )
如图,矩形ABCD的对角线AC=20,BC=16,则图中五个小矩形的周长之和为( )
 如图,矩形ABCD的对角线AC=20,BC=16,则图中五个小矩形的周长之和为( )
如图,矩形ABCD的对角线AC=20,BC=16,则图中五个小矩形的周长之和为( )| A. | 32 | B. | 36 | C. | 40 | D. | 56 |
15.下列命题是真命题的是( )
| A. | 同旁内角互补 | B. | 相等的角是对顶角 | ||
| C. | 在同一平面内,如果a∥b,b∥c,则a∥c | D. | 在同一平面内,如果a⊥b,b⊥c,则a⊥c |

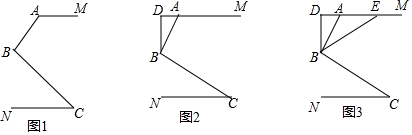
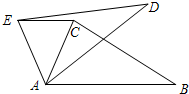 如图,△ABC中,∠CAB=70°,将△ABC绕点A旋转得到△ADE,连接CE,若AB∥EC,则∠CAD的度数为30°.
如图,△ABC中,∠CAB=70°,将△ABC绕点A旋转得到△ADE,连接CE,若AB∥EC,则∠CAD的度数为30°.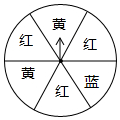 转动如图所示的转盘一次,当转盘停止转动时,记录指针所指向区域的颜色(若指针落在交界处,则重转一次)
转动如图所示的转盘一次,当转盘停止转动时,记录指针所指向区域的颜色(若指针落在交界处,则重转一次) 如图是在方格纸上画出的小旗图案,若用(1,1)表示点A,(1,5)表示点B,(2,3)表示点D,那么点C的位置可表示为(4,3).
如图是在方格纸上画出的小旗图案,若用(1,1)表示点A,(1,5)表示点B,(2,3)表示点D,那么点C的位置可表示为(4,3).