题目内容
2.已知关于x的一元二次方程x2-(m+6)x+3m+9=0的两个实数根分别为x1,x2.(1)求证:该一元二次方程总有两个实数根;
(2)若n=4(x1+x2)-x1x2,判断动点P(m,n)所形成的函数图象是否经过点A(1,16),并说明理由.
分析 (1)先求出△的值,再根据一元二次方程根的情况与判别式△的关系即可得出答案;
(2)根据n=4(x1+x2)-x1x2,求出n=m+15,即可得出动点P(m,n)所形成的函数图象经过点A(1,16).
解答 解(1)∵△=(m+6)2-4(3m+9)=m2≥0
∴该一元二次方程总有两个实数根
(2)动点P(m,n)所形成的函数图象经过点A(1,16),
∵n=4(x1+x2)-x1x2=4(m+6)-(3m+9)=m+15
∴P(m,n)为P(m,m+15).
∴A(1,16)在动点P(m,n)所形成的函数图象上.
点评 此题考查了根的判别式和根与系数的关系,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
10.已知$\frac{a}{2}$=$\frac{b}{5}$,则$\frac{b-a}{a}$的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{5}{2}$ |
7.如果|a+2|+(b-1)2=0,那么代数式(a+b)2015的值是( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 2015 |


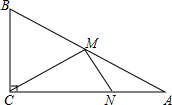 如图,在Rt△ABC中,AC=4,BC=3,若点M、N分别是线段AB、AC上的两个动点,则CM+MN的最小值为$\frac{96}{25}$.
如图,在Rt△ABC中,AC=4,BC=3,若点M、N分别是线段AB、AC上的两个动点,则CM+MN的最小值为$\frac{96}{25}$.