题目内容
10.耸立在临清市城北大运河东岸的舍利宝塔,是“运河四大名塔”之一(如图1).数学兴趣小组的小亮同学在塔上观景点P处,利用测角仪测得运河两岸上的A,B两点的俯角分别为17.9°,22°,并测得塔底点C到点B的距离为142米(A、B、C在同一直线上,如图2),求运河两岸上的A、B两点的距离(精确到1米).(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,sin17.9°≈0.31,cos17.9°≈0.95,tan17.9°≈0.32)
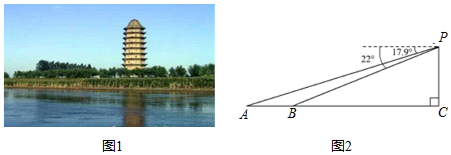
分析 在Rt△PBC中,求出BC,在Rt△PAC中,求出AC,根据AB=AC-BC计算即可.
解答 解:根据题意,BC=142米,∠PBC=22°,∠PAC=17.9°,
在Rt△PBC中,tan∠PBC=$\frac{PC}{BC}$,
∴PC=BCtan∠PBC=142•tan22°,
在Rt△PAC中,tan∠PAC=$\frac{PC}{AC}$,
∴AC=$\frac{PC}{tan∠PAC}$=$\frac{142•tan22°}{tan17.9°}$≈$\frac{142×0.40}{0.32}$≈177.5,
∴AB=AC-BC=177.5-142≈36米.
答:运河两岸上的A、B两点的距离为36米.
点评 解直角三角形的应用-仰角俯角问题、锐角三角函数等知识,解题的关键是正确寻找直角三角形,利用三角函数解决问题,属于中考常考题型.

练习册系列答案
相关题目
1.一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为( )
| A. | 120° | B. | 130° | C. | 135° | D. | 150° |
18.下列各式由左到右的变形中,属于分解因式的是( )
| A. | a(m+n)=am+an | B. | a2-b2-c2=(a-b)(a+b)-c2 | ||
| C. | 10x2-5x=5x(2x-1) | D. | x2-16+6x=(x+4)(x-4)+6x |
19. 如图为张小亮的答卷,他的得分应是( )
如图为张小亮的答卷,他的得分应是( )
 如图为张小亮的答卷,他的得分应是( )
如图为张小亮的答卷,他的得分应是( )| A. | 100分 | B. | 80分 | C. | 60分 | D. | 40分 |
20. 如图所示的圆锥的主视图是( )
如图所示的圆锥的主视图是( )
 如图所示的圆锥的主视图是( )
如图所示的圆锥的主视图是( )| A. |  | B. |  | C. |  | D. |  |
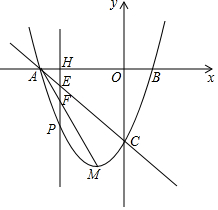 在平面直角坐标系中,已知抛物线y=x2+bx+c的顶点M的坐标为(-1,-4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
在平面直角坐标系中,已知抛物线y=x2+bx+c的顶点M的坐标为(-1,-4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.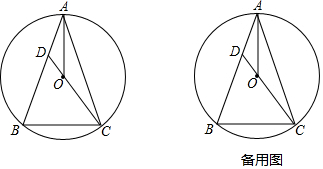
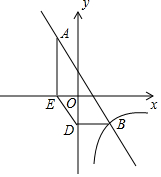 已知:如图,一次函数y=-2x+1与反比例函数y=$\frac{k}{x}$的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连接DE.
已知:如图,一次函数y=-2x+1与反比例函数y=$\frac{k}{x}$的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连接DE.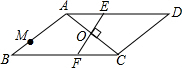 如图,在?ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点,则△AOE与△BMF的面积比为3:4.
如图,在?ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F;点M是边AB的一个三等分点,则△AOE与△BMF的面积比为3:4.