题目内容
【题目】如图1,经过原点O的抛物线![]() 与x轴交于另一点
与x轴交于另一点![]() ,在第一象限内与直线
,在第一象限内与直线![]() 交于点
交于点![]() .
.
![]() 求这条抛物线的表达式;
求这条抛物线的表达式;
![]() 在第四象限内的拋物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
在第四象限内的拋物线上有一点C,满足以B,O,C为顶点的三角形的面积为2,求点C的坐标;
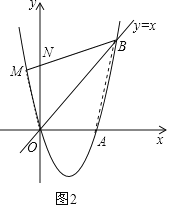
![]() 如图2,若点M在这条抛物线上,且
如图2,若点M在这条抛物线上,且![]() ,
,
![]() 求点M的坐标;
求点M的坐标;
![]() 在
在![]() 的条件下,是否存在点P,使得
的条件下,是否存在点P,使得![]() ∽
∽![]() ?若存在,求出点P的坐标;若不存在,请说明理由.
?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)抛物线解析式为![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;![]() 存在满足条件的点P,其坐标为
存在满足条件的点P,其坐标为![]() 或
或![]()
【解析】
![]() 由直线解析式可求得B点坐标,由A、B坐标,利用待定系数法可求得抛物线的表达式;
由直线解析式可求得B点坐标,由A、B坐标,利用待定系数法可求得抛物线的表达式;
![]() 过C作
过C作![]() 轴,交x轴于点E,交OB于点D,过B作
轴,交x轴于点E,交OB于点D,过B作![]() 于点F,可设出C点坐标,利用C点坐标可表示出CD的长,从而可表示出
于点F,可设出C点坐标,利用C点坐标可表示出CD的长,从而可表示出![]() 的面积,由条件可得到关于C点坐标的方程,可求得C点坐标;
的面积,由条件可得到关于C点坐标的方程,可求得C点坐标;
(3)①设MB交y轴于点N,则可证得![]() ≌
≌![]() ,可求得N点坐标,可求得直线BN的解析式,联立直线BM与抛物线解析式可求得M点坐标;
,可求得N点坐标,可求得直线BN的解析式,联立直线BM与抛物线解析式可求得M点坐标;
②过M作![]() 轴于点G,由B、C的坐标可求得OB和OC的长,由相似三角形的性质可求得
轴于点G,由B、C的坐标可求得OB和OC的长,由相似三角形的性质可求得![]() 的值,当点P在第一象限内时,过P作
的值,当点P在第一象限内时,过P作![]() 轴于点H,由条件可证得
轴于点H,由条件可证得![]() ∽
∽![]() ,由
,由![]() 的值,可求得PH和OH,可求得P点坐标;当P点在第三象限时,同理可求得P点坐标.
的值,可求得PH和OH,可求得P点坐标;当P点在第三象限时,同理可求得P点坐标.
解:![]() 在直线
在直线![]() 上,
上,
![]() ,
,
![]() ,
,
把A、B两点坐标代入抛物线解析式可得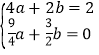 ,
,
解得![]() ,
,
![]() 抛物线解析式为
抛物线解析式为![]() ;
;
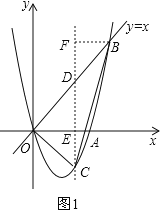
![]() 如图1,过C作
如图1,过C作![]() 轴,交x轴于点E,交OB于点D,过B作
轴,交x轴于点E,交OB于点D,过B作![]() 于点F,
于点F,
![]() 点C是抛物线上第四象限的点,
点C是抛物线上第四象限的点,
![]() 可设
可设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
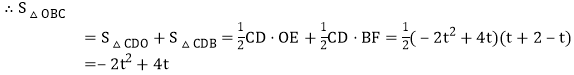 ,
,
![]() 的面积为2,
的面积为2,
![]() ,解得
,解得![]() ,
,
![]() ;
;
(3)①设MB交y轴于点N,如图2,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
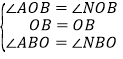 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() 可设直线BN解析式为
可设直线BN解析式为![]() ,
,
把B点坐标代入可得![]() ,解得
,解得![]() ,
,
![]() 直线BN的解析式为
直线BN的解析式为![]() ,
,
联立直线BN和抛物线解析式可得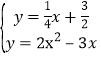 ,
,
解得![]() 或
或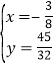 ,
,
![]() ,
,
②![]() ,
,
![]() ,且
,且![]() ,
,
![]() ,
,![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,![]() ,
,
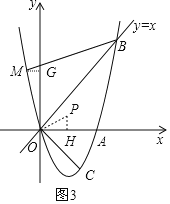
当点P在第一象限时,如图3,过M作![]() 轴于点G,过P作
轴于点G,过P作![]() 轴于点H,
轴于点H,
![]() ,
,
![]() ,且
,且![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
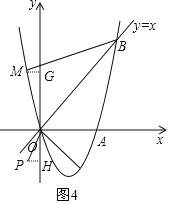
当点P在第三象限时,如图4,过M作![]() 轴于点G,过P作
轴于点G,过P作![]() 轴于点H,
轴于点H,
同理可求得![]() ,
,![]() ,
,
![]() ;
;
综上可知存在满足条件的点P,其坐标为![]() 或
或![]()

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案